第六章
6.1
由备注中的结论:
这里求双边 z 变换:
法一:直接由定义与等比数列求和公式
法二:利用微分性质
由备注中的结论有,
备注 该题使用的结论及其证明现罗列如下:
由等比数列求和公式,有:
利用线性性质与上述结论 (序列指数加权),有
6.2
其 z 变换及其收敛域为
零极点图的代码及其图像
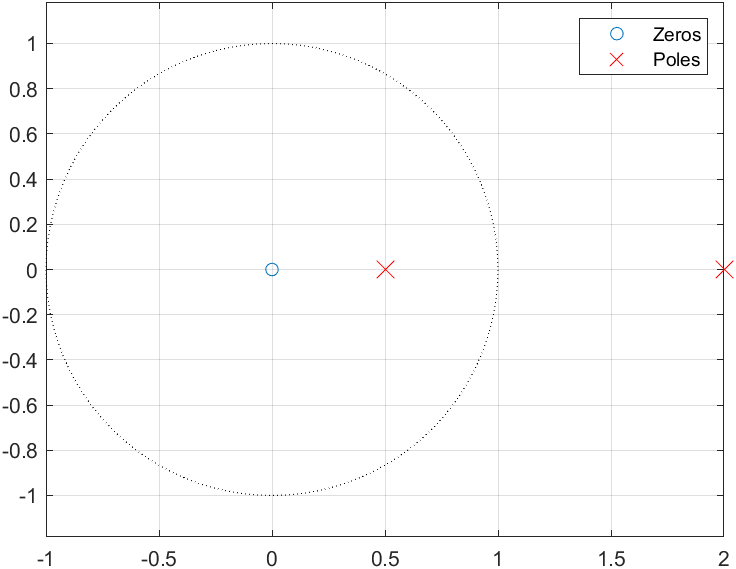
附
调用代码:
1a = [2, -5, 2];2b = [-3, 0];3plotpzd(a, b, true)函数代码:
x1function plotpzd(a, b, showCircle)2% Plot the zeros-poles distribution map3% Variable a is a denominator coefficient vector,4% and b is a nominator coefficient vector.5
6ps = roots(a); % roots of denominator polynomial7zs = roots(b); % roots of nominator polynomial8legStr = []; % legend string9
10if (~isempty(zs))11 plot(real(zs), imag(zs), 'o'); hold on;12 legStr = [legStr; 'Zeros'];13end14if (~isempty(ps))15 plot(real(ps), imag(ps), 'rx', 'markersize', 12);16 legStr = [legStr; 'Poles'];17end18if(~exist('showCircle','var'))19 showCircle = false;20end21if (showCircle)22 rectangle('position', [-1, -1, 2, 2], 'curvature', [1,1], 'LineStyle', ':')23end24
25xmin = floor(min([real(ps); real(zs)])); xmin = min(xmin, -1);26xmax = ceil(max([real(ps); real(zs)])); xmax = max(xmax, 1);27ymin = floor(min([imag(ps); imag(zs)])); ymin = min(ymin, -1);28ymax = ceil(max([imag(ps); imag(zs)])); ymax = max(ymax, 1);29axis([xmin xmax ymin ymax]), axis equal;30legend(legStr), grid on;31
32% set(gca,'YAxisLocation','origin');33% set(gca,'XAxisLocation','origin');34
35end6.3
备注
6.4
展开
于是
从而
备注 当
6.5
由长除法:
备注
有如下思路
直接求出 z 逆变化,从而得到序列的前若干项.
幂级数展开(求导法)
幂级数展开(长除法)
如果无需 z 逆变换的闭合表达式,则第三种方法一般最为简便.
这里采用前两种算法的 mathematica 代码如下:
题述函数的定义:
xxxxxxxxxx31X1[z_] := z^2/((z - 2) (z - 1))2X2[z_] := (z^2 + z + 1)/((z - 1) (z + 0.5))3X3[z_] := (z^2 - z)/(z - 1)^3求逆变换的代码:
xxxxxxxxxx31Table[InverseZTransform[X1[z], z, n], {n, 0, 2}]2Table[InverseZTransform[X2[z], z, n], {n, 0, 2}]3Table[InverseZTransform[X3[z], z, n], {n, 0, 2}]幂级数展开的代码:
xxxxxxxxxx31Series[X1[1/z], {z, 0, 2}]2Series[X2[1/z], {z, 0, 2}]3Series[X3[1/z], {z, 0, 2}]经检验,结果是一致的.
6.6
备注 当
6.7
由 6.1 备注中的结论:
备注
6.8
右边序列:
左边序列:
双边序列:
附 零极点图如下图所示:

6.9
思路一:求 z 逆变换.
因此
思路二:特值定理
由于极点绝对值大于 1,
6.10
备注 类似的,有以下结论:
6.11
思路一:利用定义,
思路二:平移性质,
思路一:利用定义——裂项相消,或者逐项求导
思路二:微分性质,由
思路三:由卷积定理可得. 实际上,由数学归纳法有
取
思路一:利用微分性质,
思路二:利用卷积定理,
见 6.10 备注,由幂级数展开得到
由
利用微分性质和尺度性质(见本题备注中的结论),有
思路一:利用定义与差比数列求和公式.
思路二:利用卷积定理(或直接由第二问中提到的结论).
思路三:利用微分性质,
思路一:利用定义,
思路二:利用时移性质.
备注
第二问标答分母次方应该为 3.
利用 6.1 备注中的结论和尺度性质(序列指数加权),
第八问标答有误.
6.12
6.13
备注 第一问应当注意收敛域;并不严谨.
6.14
备注 不想做这题.
6.15
备注
这里解出的
第三问答案似乎有误,
xxxxxxxxxx71Apart[((10 z)/(z - 1) - 0.28 + 0.08/z)/((1 + 0.1 z^-1 + 0.02 z^-2) z), z]23RSolveValue[{4y[n] + 0.1 y[n - 1] - 0.02 y[n - 2] == 10 UnitStep[n],5y[-1] == 4, y[-2] == 66}, y[n], n7] // Simplify
6.16
6.17
6.18
系统临界稳定.
思路一(直接求卷积):
思路二(用卷积定理)
6.19
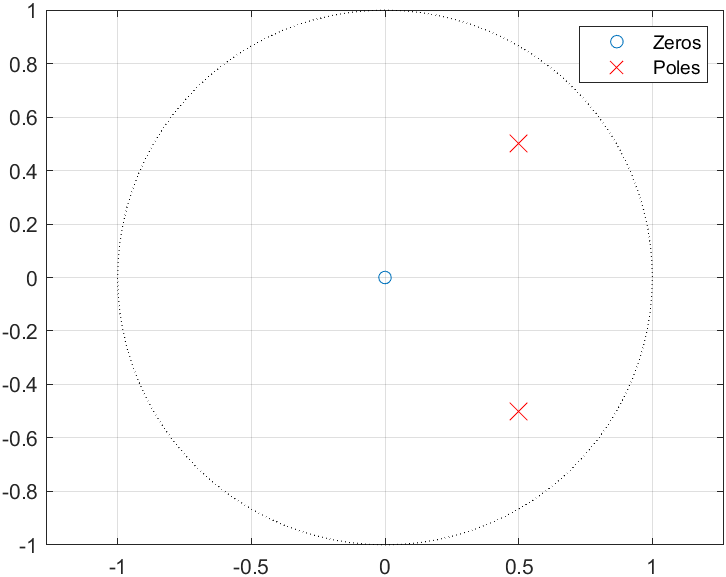
由
6.20
备注
考虑零状态响应;系统框图略.
第四问实际上有
证明 已知
(等以后补充吧.)
6.21
当
因果、不稳定.
当
非因果、稳定.
6.22
6.23
6.24 ?
6.25
故系统不稳定.