1 矢量分析与场论
1.1 矢量代数
高数笔记

1.1.1 矢量的运算
矢量的概念
这里只考虑三维的矢量(行向量).
矢量的加减
加法:.
负数:.
减法:.
矢量的乘法
数乘:.
点乘:.
叉乘:.
混合积:.
1.1.2 矢量的性质
基本性质(并不完整)
加法:零元、负元、结合律、交换律.
数乘:结合律、第一第二分配律、消去律.
点积:交换律、数乘结合律、加法分配律.
点乘
.
.
.
叉乘
叉乘性质
.
.
.
其它表示
行列式:.
行向量:.
列向量:.
混合积
.
.
向量共面 .
其它性质
1.1.3 矢量恒等式
拉格朗日恒等式
.
.
雅可比恒等式:.
四向量恒等式
.
.
.
证明
1.1.4 矢量微积分
设 ,此外 为常数, 为常向量.
求导
.
.
.
.
.
积分
.
.
.
1.1.5 矢量的旋转
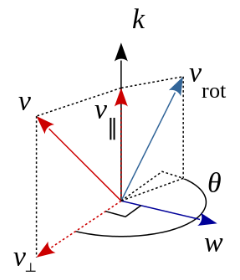
设转轴的单位方向向量为 ,旋转前的向量为 ,逆时针旋转 后的向量为 (即图中的 ),则
证明
备注 有关空间旋转的更多内容可参考笔记平面旋转与空间旋转.
1.2 常用坐标系
1.2.1 正交坐标系
基本符号
空间度量
长度元:
面积元:
体积元:.
1.2.2 直角坐标系
基本符号
坐标变量:.
单位矢量:.
位置矢量:.
空间度量
长度元:
面积元:
体积元:.
坐标变量关系
圆柱 直角:
球极 直角:
单位矢量关系
单位矢量的偏导、散度与旋度均为零.
1.2.3 圆柱坐标系
基本符号
坐标符号:.
单位矢量:.
位置矢量:.
空间度量
长度元:
面积元:
体积元:.
坐标变量关系
直角 圆柱:
球极 圆柱:
单位矢量关系
单位矢量导数(未标注的均为零)
1.2.4 球极坐标系
基本符号
坐标符号:.
单位矢量:.
位置矢量:.
空间度量
长度元:
面积元:
体积元:.
坐标变量关系
直角 球极:
圆柱 球极:
单位矢量关系
单位矢量导数(未标注的均为零)
对 求偏导:
对 求偏导:
散度:
旋度:
两个位置矢量 和 夹角的余弦为
1.3 哈密顿算子
1.3.1 正交坐标系
定义
.
.
.
推论
.
.
.
例子:设 到 的距离为 , 则 .
1.3.2 直角坐标系
1.3.3 圆柱坐标系
.
.
.
1.3.4 球极坐标系
.
.
.
1.3.5 记号与拓展
可以将哈密顿算子写成向量的形式,但此时数乘与点乘均不可交换. 以直角坐标系为例:
.
左乘
右乘
备注
.
.
.
约定
梯度、散度、旋度的优先级高于数乘、点乘与叉乘,并且从右向左计算.
例 1:.
例 2:.
向量的梯度
1.4 哈密顿算子的性质
以下均假设混合偏导连续.
1.4.1 哈密顿算子与叉乘
Hamilton 算子在右边
.
.
Hamilton 算子在中间
. 🌙
. 🌙
Hamilton 算子在左边
. 🌙
.
上述公式的推论
.
.
证明
1.4.2 哈密顿算子与梯度
标量的梯度——加减乘除与复合
.
.
.
.
标量的梯度——向量点乘与散度
. 🌙
.
.
.
向量的梯度 .
证明
1.4.3 哈密顿算子与散度
.
.
.
.
.(旋度场无源)
.
证明
1.4.4 哈密顿算子与旋度
.
.
.
.(梯度场无旋)
.
.
证明
1.4.5 哈密顿算子与积分
1.5 拉普拉斯算子
1.5.1 一般定义
1.5.2 二维空间
1.5.3 三维空间
正交坐标:.
直角坐标:.
圆柱坐标:.
球坐标系:.
1.5.4 三维矢量
证明
对于圆柱坐标系,
对于球坐标系,这里采用另一种思路,
证毕.
1.5.5 算子性质
标量函数
.
.
.
向量函数
.
.
.
证明
1.6 场论定理
1.6.1 场论的三大定理
1.6.2 两个格林恒等式
1.6.3 Helmholtz 定理
Helmholtz 定理的解释
若矢量场 单值且导数连续有界,则其由散度、旋度和边界条件唯一确定.
梯度场 由散度和在边界上的法向量唯一确定.
旋度场 由旋度和在边界上的切线分量唯一确定.
对于无界空间, 若 ,则上述面积分为零.

