2 静电场与恒定电场

2.1 静电场的基础知识

大物笔记，文件夹.

2.1.1 场强的计算与例子

• 物理概念

  • 电场力：${\mathit{F}}_{21}={\displaystyle \frac{q_1{q}_2}{4\pi {\epsilon }_0}}{\displaystyle \frac{{\mathit{e}}_R}{R^2}}={\displaystyle \frac{q_1{q}_2}{4\pi {\epsilon }_0}}{\displaystyle \frac{\mathit{R}}{R^3}}={\displaystyle \frac{q_1{q}_2}{4\pi {\epsilon }_0}}\mathbf{\nabla }{\displaystyle \frac{-1}{R}}$$\bm F_{21} = \dfrac{q_1 q_2}{4\pi \ve_0} \dfrac{\bm e_R}{R^2} = \dfrac{q_1 q_2}{4\pi \ve_0} \dfrac{\bm R}{R^3} = \dfrac{q_1 q_2}{4\pi\ve_0} \grad\dfrac{-1}{R}$.

  • 电场强度：$\mathit{E}={\displaystyle \frac{q}{4\pi {\epsilon }_0}}{\displaystyle \frac{{\mathit{e}}_R}{R^2}}={\displaystyle \frac{q}{4\pi {\epsilon }_0}}{\displaystyle \frac{\mathit{R}}{R^3}}={\displaystyle \frac{q}{4\pi {\epsilon }_0}}\mathbf{\nabla }{\displaystyle \frac{-1}{R}}$$\bm E = \dfrac{q}{4\pi \ve_0} \dfrac{\bm e_R}{R^2} = \dfrac{q}{4\pi \ve_0} \dfrac{\bm R}{R^3} = \dfrac{q}{4\pi\ve_0} \grad\dfrac{-1}{R}$.

• 约定

  • 观测点 (场点) $\mathit{r}=(x,y,z)$$\bm r = (x, y, z)$.

  • 电荷处 (源点) ${\mathit{r}}^{\prime }=(x^{\prime },y^{\prime },z^{\prime })$$\bm r' = (x', y', z')$.

• 例子

  • 无限长带电直线的电场：$E={\displaystyle \frac{\rho }{2\pi {\epsilon }_{0}r}}$$E = \dfrac{\rho}{2\pi \ve_0 r} %\bm e_r$.

  • 无限大带电平面的电场：$E={\displaystyle \frac{\sigma }{2{\epsilon }_0}}$$E = \dfrac{\sigma}{2\ve_0}$.

  • 带电圆环轴线上的电场：$E={\displaystyle \frac{qz}{4\pi {\epsilon }_0(z^2+r^2{)}^{\frac{3}{2}}}}$$E = \dfrac{qz}{4\pi \ve_0 (z^2 + r^2)^{\frac{3}{2}}}$.

2.1.2 场强的通量与散度

真空中静电场的高斯定理：

• 场强 $\mathit{E}$$\bm E$

  • 积分形式：${\displaystyle {\oint }_S\mathit{E}\mathbf{\cdot }\mathrm{d}\mathit{S}={\displaystyle \frac{Q}{{\epsilon }_0}}}$$\d\oint_S \bm E \bm\cdot \dd{\bm S} = \dfrac{Q}{\ve_0}$.

  • 微分形式：$\mathbf{\nabla }\mathbf{\cdot }\mathit{E}={\displaystyle \frac{\rho }{{\epsilon }_0}}$$\div \bm E = \dfrac{\rho}{\ve_0}$.

• 电位移矢量 $\mathit{D}={\epsilon }_0\mathit{E}$$\bm D = \ve_0 \bm E$

  • 积分形式：${\displaystyle {\oint }_S\mathit{D}\mathbf{\cdot }\mathrm{d}\mathit{S}=Q}$$\d\oint_S \bm D \bm\cdot \dd{\bm S} = Q$.

  • 微分形式：$\mathbf{\nabla }\mathbf{\cdot }\mathit{D}=\rho$$\div \bm D = \rho$.

2.1.3 场强的环量与旋度

真空中静电场的斯托克斯定理：

• ${\displaystyle {\oint }_l\mathit{E}\mathbf{\cdot }\mathrm{d}\mathit{l}=0}$$\d\oint_l \bm E \bm\cdot \dd{\bm l} = 0$.

• $\mathbf{\nabla }\times \mathit{E}=\mathbf{0}$$\curl \bm E = \bm 0$.

2.1.4 静电场的电位函数

• 一般的：$\mathit{E}=-\mathbf{\nabla }\phi$$\bm E = -\grad \varphi$.

• 点电荷：$\phi ={\displaystyle \frac{q}{4\pi {\epsilon }_{0}R}}$$\varphi = \dfrac{q}{4\pi\ve_0 R}$.

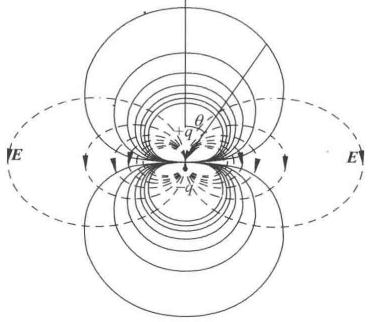
2.1.5 电偶极子和电场线

• 电偶极距 ${\mathit{P}}_{\mathrm{e}}=q\mathit{l}$$\bm P_\e = q \bm l$.

  • 要求点电荷等值异号、相距很近.

  • 方向由负电荷指向正电荷.

• 电位函数 $\phi ={\displaystyle \frac{ql\cos \theta }{4\pi {\epsilon }_0{r}^2}}={\displaystyle \frac{{\mathit{P}}_{\mathrm{e}}\cdot {\mathit{e}}_r}{4\pi {\epsilon }_0{r}^2}}$$\varphi = \dfrac{ql\cos\theta}{4\pi\ve_0 r^2} = \dfrac{\bm P_\e \cdot \bm e_r}{4\pi \ve_0 r^2}$.

  • 要求观察点远离电偶极子.

  • 等位面 $\phi ={\phi }_0\Rightarrow r^2={\displaystyle \frac{ql\cos \theta }{4\pi {\epsilon }_0{\phi }_0}}$$\varphi = \varphi_0 \RA r^2 = \dfrac{ql \cos\theta}{4\pi\ve_0\varphi_0}$.

  • 电偶极子的电位衰减快于单个电子.

• 电场强度 $\mathit{E}={\displaystyle \frac{P_{\mathrm{e}}\cos \theta }{2\pi {\epsilon }_0{r}^3}}{\mathit{e}}_r+{\displaystyle \frac{P_{\mathrm{e}}\sin \theta }{4\pi {\epsilon }_0{r}^3}}{\mathit{e}}_{\theta }$$\bm E = \dfrac{P_\e \cos\theta}{2\pi\ve_0 r^3} \bm e_r + \dfrac{P_\e\sin\theta}{4\pi\ve_0 r^3} \bm e_\theta$.

  • 要求观察点远离电偶极子.

  • 电场线 $\mathit{E}\times \mathrm{d}\mathit{l}=0\Rightarrow r=C{\sin }^2\theta$$\bm E \cp \dd{\bm l} = 0 \RA r = C\sin^2\theta$.

  • 电偶极子的场强衰减快于单个电子.

2.2 介质中的静电场

2.2.1 极化强度与极化电荷密度

• 极化强度

  • 极化强度定义：$\mathit{P}:=\underset{\mathrm{\Delta }V\to 0}{lim}{\displaystyle \sum _{i=1}^n{\displaystyle \frac{{\mathit{P}}_i}{\mathrm{\Delta }V}}}$$\bm P := \liml_{\Delta V \to 0} \insum \dfrac{\bm P_i}{\Delta V}$.

  • 一般通过另一种定义计算：$\mathit{P}\equiv {\epsilon }_0{\chi }_{\mathrm{e}}\mathit{E}$$\bm P \equiv \ve_0 \chi_\e \bm E$.

• 电介质中的电位

  • $\phi ={\displaystyle \frac{1}{4\pi {\epsilon }_0}}{\displaystyle {\oint }_{S^{\prime }}{\displaystyle \frac{\mathit{P}\cdot {\mathit{e}}_{\text{n}}\mathrm{d}{S}^{\prime }}{R}}-{\displaystyle \frac{1}{4\pi {\epsilon }_0}}{\int }_{V^{\prime }}{\displaystyle \frac{{\mathbf{\nabla }}^{\prime }\cdot \mathit{P}}{R}}\mathrm{d}{V}^{\prime }}$$\varphi = \dfrac{1}{4\pi\ve_0} \d\oint_{S'} \dfrac{\bm P \cdot \bm e_\text n \dd{S'}}{R} - \dfrac{1}{4\pi\ve_0} \int_{V'} \dfrac{\grad' \cdot \bm P}{R} \dd{V'}$.

  • ${\displaystyle \phi ={\oint }_{S^{\prime }}{\displaystyle \frac{{\rho }_{\text{p}}\mathrm{d}{S}^{\prime }}{4\pi {\epsilon }_{0}R}}+{\int }_{V^{\prime }}{\displaystyle \frac{{\rho }_{\text{ps}}\mathrm{d}{V}^{\prime }}{4\pi {\epsilon }_{0}R}}}$$\d \varphi = \oint_{S'} \dfrac{\rho_\text p \dd{S'}}{4\pi\ve_0 R} + \int_{V'} \dfrac{\rho_\text{ps} \dd{V'}}{4\pi\ve_0 R}$.

• 极化电荷密度

  • 极化电荷体密度 ${\rho }_{\text{p}}=-\mathbf{\nabla }\mathbf{\cdot }\mathit{P}$$\rho_\text p = -\div \bm P$.

  • 极化电荷面密度 ${\rho }_{\text{ps}}=\mathit{P}\mathbf{\cdot }{\mathit{e}}_{\text{n}}$$\rho_\text{ps} = \bm P \vdot \bm e_\text n$.

• 总束缚电荷 $Q=Q_{\text{p}}+Q_{\text{ps}}$$Q = Q_\text{p} + Q_\text{ps}$.

2.2.2 电位移矢量的通量与散度

• 电位移矢量

  • 考虑 $\mathbf{\nabla }\mathbf{\cdot }\mathit{E}={\displaystyle \frac{\rho +{\rho }_{\text{p}}}{{\epsilon }_0}}={\displaystyle \frac{\rho -\mathbf{\nabla }\mathbf{\cdot }\mathit{P}}{{\epsilon }_0}}$$\div \bm E = \dfrac{\rho + \rho_\text p}{\ve_0} = \dfrac{\rho - \div \bm P}{\ve_0}$.

  • 于是定义电位移矢量 $\mathit{D}:={\epsilon }_0\mathit{E}+\mathit{P}$$\bm D := \ve_0 \bm E + \bm P$.

• 介质中的高斯定理

  • 微分形式：$\mathbf{\nabla }\mathbf{\cdot }\mathit{D}=\rho$$\div \bm D %= \div (\ve_0 \bm E + \bm P) = \rho$.

  • 积分形式：${\displaystyle {\oint }_S\mathit{D}\cdot \mathrm{d}\mathit{S}=Q}$$\d\oint_S \bm D \cdot \dd{\bm S} %= \int_V \div \bm D \dd{V} = \int_V \rho \dd{V} = Q$.

2.2.3 极化强度与相对介电常数

• 极化强度：$\mathit{P}\equiv {\epsilon }_0{\chi }_{\mathrm{e}}\mathit{E}$$\bm P \equiv \ve_0 \chi_\e \bm E$.

  • 由此定义的介质的极化率 ${\chi }_{\mathrm{e}}$$\chi_\e$ 无量纲.

  • 对于线性介质, ${\chi }_{\mathrm{e}}$$\chi_\e$ 与 $\mathit{E}$$\bm E$ 无关.

  • 对于非线性介质, ${\chi }_{\mathrm{e}}$$\chi_\e$ 是 $\mathit{E}$$\bm E$ 的函数.

  • 对于各向同性的介质, ${\chi }_{\mathrm{e}}$$\chi_\e$ 是一个系数.

  • 对于各向异性的截止, ${\chi }_{\mathrm{e}}$$\chi_\e$ 是一个张量.

• 电位移矢量：$\mathit{D}={\epsilon }_0(1+{\chi }_{\mathrm{e}})\mathit{E}\equiv {\epsilon }_0{\epsilon }_{\text{r}}\mathit{E}\equiv \epsilon \mathit{E}$$\bm D = \ve_0(1 + \chi_\e) \bm E \equiv \ve_0 \ve_\text r \bm E \equiv \ve \bm E$.

  • 相对介电常数 ${\epsilon }_{\text{r}}$$\ve_\text r$ 无量纲.

  • 介电常数 $\epsilon :={\epsilon }_0{\epsilon }_{\text{r}}$$\ve := \ve_0 \ve_\text r$ 单位为 $\mathrm{F}/\mathrm{m}$$\mathrm{F / m}$.

  • 三个基本电磁参数：介电常数、磁导率、电导率.

  • 上式也称为介质中的电场物质 (本构) 方程.

  • 在真空中 ${\epsilon }_0=1$$\ve_0 = 1$, 在介质中 ${\epsilon }_0>1$$\ve_0 > 1$.

2.2.4 极化强度与极化电荷计算

• 相互关系与矢量方向

  • 电场强度 $\mathit{E}$$\bm E$、极化强度 $\mathit{P}$$\bm P$ 和电位移 $\mathit{D}$$\bm D$ 之间是线性关系.

  • $\mathit{D}$$\bm D$ 线由正的自由电荷发出, 终止于负的自由电荷.

  • $\mathit{E}$$\bm E$ 线的起止点可以在自由电荷上, 也可以在极化电荷上.

  • $\mathit{P}$$\bm P$ 线由负的极化电荷发出, 终止于正的极化电荷.

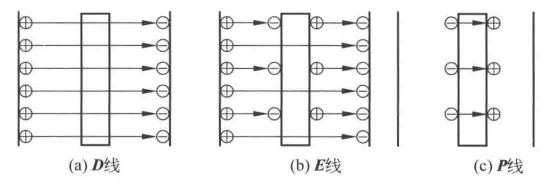
• 极化强度和极化电荷的计算

  $$\begin{array}{rl}\mathit{P}& ={\epsilon }_0{\chi }_e\mathit{E}={\epsilon }_0({\epsilon }_{\text{r}}-1)\mathit{E}={\displaystyle \frac{{\epsilon }_{\text{r}}-1}{{\epsilon }_{\text{r}}}}\mathit{D},\\ {\rho }_{\text{p}}& =-\mathbf{\nabla }\mathbf{\cdot }\mathit{P}=-{\displaystyle \frac{{\epsilon }_{\text{r}}-1}{{\epsilon }_{\text{r}}}}\mathbf{\nabla }\mathbf{\cdot }\mathit{D}-\mathit{D}\cdot \mathbf{\nabla }{\displaystyle \frac{{\epsilon }_{\text{r}}-1}{{\epsilon }_{\text{r}}}}\\ & =-{\displaystyle \frac{{\epsilon }_{\text{r}}-1}{{\epsilon }_{\text{r}}}}\rho -\mathit{D}\cdot \mathbf{\nabla }{\displaystyle \frac{{\epsilon }_{\text{r}}-1}{{\epsilon }_{\text{r}}}},\\ {\rho }_{\text{ps}}& =\mathit{P}\cdot {\mathit{e}}_{\text{n}}={\displaystyle \frac{{\epsilon }_{\text{r}}-1}{{\epsilon }_{\text{r}}}}\mathit{D}\cdot {\mathit{e}}_{\text{n}}.\end{array}$$

  对于线性各向同性介质，${\rho }_{\text{p}}={\displaystyle \frac{1-{\epsilon }_{\text{r}}}{{\epsilon }_{\text{r}}}}\rho$$\rho_\text p = \dfrac{1-\ve_\text r}{\ve_\text r} \rho$.

• 例子：真空中半径为 $a$$a$、介电常数为 $\epsilon$$\ve$ 的介质球内体电荷均匀分布，密度为 $\rho$$\rho$，则球内

  • 极化强度的计算：$\mathit{P}={\displaystyle \frac{{\epsilon }_{\text{r}}-1}{{\epsilon }_{\text{r}}}}\mathit{D}={\displaystyle \frac{{\epsilon }_{\text{r}}-1}{3{\epsilon }_{\text{r}}}}r\rho {\mathit{e}}_r$$\bm P = \dfrac{\ve_\text r - 1}{\ve_\text r} \bm D = \dfrac{\ve_\text r - 1}{3 \ve_\text r} r \rho \bm e_r$.

  • 极化电荷体密度：${\rho }_{\text{p}}=-\mathbf{\nabla }\mathbf{\cdot }\mathit{P}={\displaystyle \frac{1-{\epsilon }_{\text{r}}}{{\epsilon }_{\text{r}}}}\rho$$\rho_\text p = -\div \bm P = \dfrac{1 - \ve_\text r}{\ve_\text r} \rho$.

  • 极化电荷面密度：${\rho }_{\text{ps}}=\mathit{P}\mathbf{\cdot }{\mathit{e}}_{\text{n}}={\displaystyle \frac{{\epsilon }_{\text{r}}-1}{3{\epsilon }_{\text{r}}}}a\rho$$\rho_\text{ps} = \bm P \bm\cdot \bm e_\text n = \dfrac{\ve_\text r - 1}{3\ve_\text r} a \rho$.

  • 总束缚电荷为零：$Q={\displaystyle \frac{4\pi a^3}{3}}{\rho }_{\text{p}}+4\pi a^2{\rho }_{\text{ps}}=0$$Q = \dfrac{4\pi a^3}{3} \rho_\text p + 4\pi a^2 \rho_\text{ps} = 0$.

2.2.5 泊松方程与拉普拉斯方程

对于线性、均匀、各向同行的介质材料，$\epsilon$$\ve$ 为常数，因此有：

• 泊松方程 $\mathrm{\Delta }\phi ={\mathbf{\nabla }}^2\phi =\mathbf{\nabla }\mathbf{\cdot }(\mathbf{\nabla }\phi )=\mathbf{\nabla }\mathbf{\cdot }(-\mathit{E})=\mathbf{\nabla }\mathbf{\cdot }(-{\displaystyle \frac{\mathit{D}}{\epsilon }})=-{\displaystyle \frac{\rho }{\epsilon }}$$\Delta \varphi = \grad^2 \varphi = \div (\grad \varphi) = \div (-\bm E) = \div \pqty{-\dfrac{\bm D}{\ve}} = -\dfrac{\rho}{\ve}$.

• 当空间中没有电荷时, 泊松方程变为拉普拉斯方程 $\mathrm{\Delta }\phi =0$$\Delta \varphi = 0$.

2.3 静电场的边界条件

2.3.1 电位移法向边界条件

• 法向边界条件

  • ${\rho }_{\text{s}}={\mathit{e}}_{\text{n}}\cdot ({\mathit{D}}_1-{\mathit{D}}_2)$$\rho_\text s = \bm e_\text n \cdot (\bm D_1 - \bm D_2)$.

  • ${\rho }_{\text{s}}=D_{1\text{n}}-D_{2\text{n}}={\epsilon }_1{E}_{1\text{n}}-{\epsilon }_2{E}_{2\text{n}}$$\rho_\text s = D_{1\text n} - D_{2\text n} = \ve_1 E_{1\text n} - \ve_2 E_{2 \text n} %= -\ve_1 \d\pdv{\phi_1}{n} + \ve_2 \pdv{\phi_1}{n}$.

  • 其中 ${\rho }_{\text{s}}$$\rho_\text s$ 是自由面电荷密度，而非极化面电荷密度.

• 特例与说明

  • 可由此计算极化电荷面密度.

  • 若有一个媒质是导体，则 $D_{\text{n}}={\rho }_{\text{s}}$$D_\text n = \rho_\text s$.

  • 如果导体表面有自由面电荷，则电场与表面垂直.

2.3.2 场强的切向边界条件

• 切向边界条件

  • $({\mathit{E}}_1-{\mathit{E}}_2)\cdot {\mathit{e}}_{\text{t}}=0$$(\bm E_1 - \bm E_2) \cdot \bm e_\text t = 0$.

  • $({\mathit{E}}_1-{\mathit{E}}_2)\times {\mathit{e}}_{\text{n}}=\mathbf{0}$$(\bm E_1 - \bm E_2) \cp \bm e_\text n = \bm 0$.

  • $E_{\text{1t}}=E_{\text{2t}}={\displaystyle \frac{D_{\text{1t}}}{{\epsilon }_1}}={\displaystyle \frac{D_{2\text{t}}}{{\epsilon }_2}}$$E_\text{1t} = E_\text{2t} = \dfrac{D_\text{1t}}{\ve_1} = \dfrac{D_{2\text t}}{\ve_2}$.

• 特例与说明

  • 若有一个媒质是导体，则 $E_{\text{t}}=0$$E_\text t = 0$.

  • 电场在导体表面没有切向分量.

2.3.3 电位函数的边界条件

• 电位函数连续，即 ${\phi }_1={\phi }_2$$\varphi_1 = \varphi_2$.

• ${\rho }_{\text{s}}={\epsilon }_2{\displaystyle \frac{\partial {\varphi }_2}{\partial n}-{\epsilon }_1\frac{\partial {\varphi }_1}{\partial n}}$$\rho_\text s = \ve_2 \d\pdv{\phi_2}{n} - \ve_1 \pdv{\phi_1}{n}$.

• 上式中注意方向.

2.3.4 分界面上的电场方向

• 若分界面上没有自由电荷，即 ${\rho }_{\text{s}}=0$$\rho_\text s = 0$，则

  • ${\displaystyle \frac{\tan {\theta }_1}{\tan {\theta }_2}}={\displaystyle \frac{{\epsilon }_1}{{\epsilon }_2}}$$\dfrac{\tan\theta_1}{\tan\theta_2} = \dfrac{\ve_1}{\ve_2}$.

  • ${\displaystyle \frac{E_1}{E_2}}={\displaystyle \frac{\cos {\theta }_2}{\cos {\theta }_1}}$$\dfrac{E_1}{E_2} = \dfrac{\cos\theta_2}{\cos\theta_1}$.

• 其中角度为场强与法线的夹角.

2.3.5 电荷密度的计算方法

• 自由电荷

  • 自由体电荷密度：$\rho =\mathbf{\nabla }\mathbf{\cdot }\mathit{D}$$\rho = \div \bm D$.

  • 自由面电荷密度：${\rho }_{\text{s}}=({\mathit{D}}_1-{\mathit{D}}_2)\mathbf{\cdot }\mathit{n}$$\rho_\text s = (\bm D_1 - \bm D_2) \bm\cdot \bm n$.

• 束缚电荷

  • 极化体电荷密度：${\rho }_{\text{p}}=-\mathbf{\nabla }\mathbf{\cdot }\mathit{P}$$\rho_\text{p} = -\div \bm P$.

  • 极化面电荷密度：${\rho }_{\text{ps}}=\mathit{P}\mathbf{\cdot }\mathit{n}$$\rho_\text{ps} = \bm P \bm\cdot \bm n$.

2.5 静电场的其它问题

2.5.1 双导体与孤立导体电容

• 电容定义

  • 双导体 $C={\displaystyle \frac{q}{U}}$$C = \dfrac{q}{U}$.

  • 孤立导体 $C={\displaystyle \frac{q}{\phi }}$$C = \dfrac{q}{\varphi}$.

• 电容求解

  • 法一：假设 $q$$q$，求出 $\mathit{E}$$\bm E$ 从而积分得到 $U$$U$.

  • 法二：假设 $\phi$$\varphi$，求出 $\mathit{E}$$\bm E$ 从而得到 $q$$q$（考虑体电荷、面电荷）

2.5.2 常见导体系统电容公式

• 双导体

  • 平板电容器：$C={\displaystyle \frac{\epsilon S}{d}}$$C = \dfrac{\ve S}{d}$.

  • 同轴圆柱：$C=2\pi \epsilon l/\ln \frac{b}{a}$$C = {2\pi\ve l} \left/ {\ln\cfrac{b}{a}} \right.$.

  • 同心球壳：$C={\displaystyle \frac{4\pi \epsilon ab}{b-a}}$$C = \dfrac{4\pi\ve ab}{b-a}$.

  • 远距两球：$C={\displaystyle \frac{4\pi {\epsilon }_0}{\frac{1}{a}+\frac{1}{b}-\frac{2}{d}}}$$C = \dfrac{4\pi\ve_0}{\cfrac{1}{a} + \cfrac{1}{b} - \cfrac{2}{d}}$.

• 孤立电容

  • 球体 / 薄球壳：$C=4\pi \epsilon R$$C = 4\pi\ve R$.

2.5.3 多导体系统的部分电容

• 假设各导体的电量为 $q_0,\cdots ,q_n$$q_0, \cdots, q_n$, 电位为 ${\phi }_0,\cdots ,{\phi }_n$$\varphi_0, \cdots, \varphi_n$, 且 ${\phi }_0=0$$\varphi_0 = 0$.

• $q_k={\displaystyle \sum _{s=1}^n{\beta }_{sk}{\phi }_s}$$q_k = \dsum_{s=1}^n \beta_{sk} \varphi_s$.

  • ${\beta }_{sk}$$\beta_{sk}$ 称为电容系数,

  • 当 $s=k$$s = k$ 时称为自电容系数,

  • 当 $s\ne k$$s \ne k$ 时称为互电容系数.

• $q_k={\displaystyle \sum _{s=1}^{k-1}{C}_{ks}({\phi }_k-{\phi }_s)+C_{kk}{\phi }_k+\sum _{s=k+1}^n{C}_{ks}({\phi }_k-{\phi }_s)}$$q_k = \dsum_{s = 1}^{k - 1} C_{ks}(\varphi_k - \varphi_s) + C_{kk} \varphi_k + \sum_{s = k + 1}^n C_{ks}(\varphi_k - \varphi_s)$.

  • $C_{ks}$$C_{ks}$ 称为部分电容.

  • 当 $s=k$$s = k$ 时称为自部分电容, 即全部导体的电位都是一个单位时, 第 $k$$k$ 个导体上的总电荷量.

  • 当 $s\ne k$$s \ne k$ 时称为互部分电容, 即第 $s$$s$ 个导体上的电位为一个单位, 其它导体接地时, 第 $k$$k$ 个导体上的总电荷量.

  • $C_{ks}=C_{sk}>0$$C_{ks} = C_{sk} > 0$.

  • 两导体间的等效电容不一定等于部分电容.

2.5.4 静电场的能量及其密度

• 静电场的能量

  • 离散形式：$W_{\text{e}}={\displaystyle \frac{1}{2}}{\displaystyle \sum _i{\phi }_i{q}_i}$$W_\text e = \dfrac{1}{2} \dsum_i \varphi_i q_i$.

  • 体积积分：$W_{\mathrm{e}}={\displaystyle \frac{1}{2}}{\displaystyle {\int }_V\rho \phi \mathrm{d}V}$$W_\e = \dfrac{1}{2} \dint_V \rho \varphi \dd{V}$

  • 面积积分：$W_{\mathrm{e}}={\displaystyle \frac{1}{2}}{\displaystyle {\int }_S{\rho }_{\text{s}}\phi \mathrm{d}S}$$W_\e = \dfrac{1}{2} \dint_S \rho_\text s \varphi \dd{S}$.

• 静电场的能量密度

  • $W_{\mathrm{e}}={\displaystyle \frac{1}{2}}{\displaystyle {\int }_V\mathit{D}\mathbf{\cdot }\mathit{E}\mathrm{d}V={\displaystyle \frac{1}{2}}{\displaystyle {\int }_V{\omega }_{\mathrm{e}}\mathrm{d}V}}$$W_\e = \dfrac{1}{2} \dint_V \bm D \bm\cdot \bm E \dd{V} = \dfrac{1}{2} \dint_V \omega_\e \dd{V}$.

  • ${\omega }_{\mathrm{e}}={\displaystyle \frac{\mathit{D}\mathbf{\cdot }\mathit{E}}{2}}={\displaystyle \frac{\epsilon E^2}{2}}={\displaystyle \frac{D^2}{2\epsilon }}$$\omega_\e = \dfrac{\bm D \bm\cdot \bm E}{2} = \dfrac{\ve E^2}{2} = \dfrac{D^2}{2\ve}$.

• 电容系统的能量：$W_{\mathrm{e}}={\displaystyle \frac{C{U}^2}{2}}={\displaystyle \frac{q^2}{2C}}$$W_\e = \dfrac{CU^2}{2} = \dfrac{q^2}{2C}$.

2.5.5 计算静电力的虚位移法

对于复杂系统，利用 $\mathrm{d}W=F\mathrm{d}x+\mathrm{d}{W}_{\mathrm{e}}$$\dd{W} = F \dx + \dd{W_\e}$.

• 若各带电导体的电位不变

  • $\mathrm{d}W={\displaystyle \sum _i{\phi }_i\mathrm{d}{q}_i}$$\dd{W} = \dsum_i \varphi_i \dd{q_i}$.

  • $\mathrm{d}{W}_{\mathrm{e}}={\displaystyle \frac{1}{2}}{\displaystyle \sum _i{\phi }_i\mathrm{d}{q}_i}$$\dd{W_\e} = \dfrac{1}{2} \dsum_i \varphi_i \dd{q_i}$.

  • $F={{\displaystyle \frac{\partial W_{\mathrm{e}}}{\partial x}\phantom{\int }}|}_{\phi =\text{常}\text{数}}$$F = \eval{\dpdv{W_\e}{x}}_{\varphi = 常数}$.

• 若各带电导体的电荷不变

  • $\mathrm{d}W=0$$\dd{W} = 0$.

  • $F=-{{\displaystyle \frac{\partial W_{\mathrm{e}}}{\partial x}\phantom{\int }}|}_{q=\text{常}\text{数}}$$F = -\eval{\dpdv{W_\e}{x}}_{q = 常数}$.

2.6 恒定电场

2.6.1 电流与电流密度矢量

• 自由电流

  • 传导电流：导体、导电溶液、半导体中.

  • 运流电流：真空、气体中.

• 电流密度

  • 体电流 $\left|\mathit{J}\right|={\displaystyle \frac{\mathrm{d}I}{\mathrm{d}S}}$$\vqty{\bm J} = \ddv{I}{S}$.

  • 面电流 $\left|{\mathit{J}}_s\right|={\displaystyle \frac{\mathrm{d}I}{\mathrm{d}l}}$$\vqty{\bm J_s} = \ddv{I}{l}$.

  • $\mathit{J}=\left|\mathit{J}\right|{\mathit{e}}_{{}_{\mathit{J}}}=\rho \mathit{v}$$\bm J = \vqty{\bm J} \bm e_{_\bm J} = \rho \bm v$.

• 电流强度 (电流密度通量)

  • 定义式：$I={\displaystyle \frac{\mathrm{d}q}{\mathrm{d}t}}$$I = \ddv{q}{t}$.

  • 体电流：$I={\displaystyle {\int }_S\mathit{J}\mathbf{\cdot }\mathrm{d}\mathit{S}}$$I = \dint_S \bm J \bm\cdot \dd{\bm S}$

  • 面电流：$I={\displaystyle {\int }_l{\mathit{J}}_s\mathbf{\cdot }\mathrm{d}\mathit{l}}$$I = \dint_l \bm J_s \bm\cdot \dd{\bm l}$.

2.6.2 恒定电场的基本性质

• 电流连续性方程

  • 一般形式（电荷守恒定律）

    • 积分形式：${\displaystyle {\oint }_S\mathit{J}\mathbf{\cdot }\mathrm{d}\mathit{S}=-\frac{\partial q}{\partial t}}$$\d\oint_S \bm J \bm\cdot \dd{\bm S} = -\pdv{q}{t}$.

    • 微分形式：$\mathbf{\nabla }\mathbf{\cdot }\mathit{J}=-{\displaystyle \frac{\partial \rho }{\partial t}}$$\div \bm J = -\dpdv{\rho}{t}$.

  • 恒定电场（基尔霍夫电流定律）

    • 积分形式：${\displaystyle {\oint }_S\mathit{J}\mathbf{\cdot }\mathrm{d}\mathit{S}=0}$$\d\oint_S \bm J \bm\cdot \dd{\bm S} = 0$.

    • 微分形式：$\mathbf{\nabla }\mathbf{\cdot }\mathit{J}=0$$\div \bm J = 0$.

• 恒定电场的无旋性（基尔霍夫电压定律）

  • 积分形式：${\displaystyle {\oint }_l\mathit{E}\mathbf{\cdot }\mathrm{d}\mathit{l}=0}$$\d\oint_l \bm E \bm\cdot \dd{\bm l} = 0$.

  • 微分形式：$\mathbf{\nabla }\times \mathit{E}=\mathbf{0}$$\curl \bm E = \bm 0$.

  • 电位函数：$\mathit{E}=-\mathbf{\nabla }\varphi$$\bm E = -\grad \phi$.

• 欧姆定律

  • 公式

    • 微分形式：$\mathit{J}\equiv \sigma \mathit{E}$$\bm J \equiv \sigma \bm E$.

    • 积分形式：$U={\displaystyle \frac{Il}{\sigma S}}\equiv IR$$U = \dfrac{Il}{\sigma S} \equiv IR$.

  • 说明

    • 电导率 $\sigma$$\sigma$ 单位为 $\mathrm{S}/\mathrm{m}$$\rm{S/m}$.

    • 电源内部：$\mathit{J}=\sigma (\mathit{E}+{\mathit{E}}^{\prime })$$\bm J = \sigma (\bm E + \bm E')$.

    • 长直导线电阻：$R={\displaystyle \frac{l}{\sigma S}}$$R = \dfrac{l}{\sigma S}$.

• 恒定电场的无散性

  • $\mathbf{\nabla }\mathbf{\cdot }\left(\sigma \mathit{E}\right)=0\Rightarrow \mathbf{\nabla }\mathbf{\cdot }\mathit{E}=-\mathit{E}\mathbf{\cdot }{\displaystyle \frac{\mathbf{\nabla }\sigma }{\sigma }}$$\div (\sigma \bm E) = 0 \RA \div \bm E = -\bm E \bm\cdot \dfrac{\grad \sigma}{\sigma}$.

  • $\rho =\mathbf{\nabla }\mathbf{\cdot }\left(\epsilon \mathit{E}\right)=\mathit{E}\mathbf{\cdot }(\mathbf{\nabla }\epsilon -{\displaystyle \frac{\epsilon }{\sigma }}\mathbf{\nabla }\sigma )$$\rho = \div(\ve \bm E) = \bm E \bm\cdot \pqty{\grad \ve - \dfrac{\ve}{\sigma} \grad \sigma}$.

• 线性均匀媒质

  • $\mathbf{\nabla }\mathbf{\cdot }\mathit{E}=0,\rho =0$$\div \bm E = 0,\ \rho = 0$.

  • $\mathrm{\Delta }\phi =-\mathbf{\nabla }\mathbf{\cdot }\mathit{E}=0$$\Delta \varphi = -\div \bm E = 0$.

2.6.3 恒定电场的边界条件

• 积分：场强与电流密度

  • 法向边界条件

    • $({\mathit{J}}_1-{\mathit{J}}_2)\cdot {\mathit{e}}_{\text{n}}=0$$(\bm J_1 - \bm J_2) \cdot \bm e_\text n = 0$.

    • $J_{1\text{n}}=J_{2\text{n}}$$J_{1\text n} = J_{2\text n}$.

  • 切向边界条件

    • ${\mathit{e}}_{\text{n}}\times ({\mathit{E}}_1-{\mathit{E}}_2)=0$$\bm e_\text n \cp (\bm E_1 - \bm E_2) = 0$.

    • $E_{1\text{t}}=E_{2\text{t}}$$E_{1\text t} = E_{2\text t}$.

• 推论：电位与折线夹角

  • 电位函数连续

    • ${\varphi }_1={\varphi }_2$$\phi_1 = \phi_2$.

    • ${\sigma }_1{\displaystyle \frac{\partial {\varphi }_1}{\partial n}={\sigma }_2\frac{\partial {\varphi }_2}{\partial n}}$$\sigma_1 \d\pdv{\phi_1}{n} = \sigma_2 \pdv{\phi_2}{n}$.

  • 电流矢量折线

    • ${\displaystyle \frac{\tan {\theta }_1}{\tan {\theta }_2}}={\displaystyle \frac{{\sigma }_1}{{\sigma }_2}}$$\dfrac{\tan\theta_1}{\tan\theta_2} = \dfrac{\sigma_1}{\sigma_2}$，其中角度为电流矢量与法线的夹角.

    • 良导体（$\sigma$$\sigma$ 大）的电流流入不良导体，则流出电流近似垂直于分界面，于是良导体表面可以近似地看作等位面.

• 自由电荷分布

  • 不均匀的导电媒质在恒定电场中：$\rho =\mathbf{\nabla }\mathbf{\cdot }\mathit{D}=\mathit{J}\mathbf{\cdot }\mathbf{\nabla }{\displaystyle \frac{\epsilon }{\sigma }}$$\rho = \div \bm D = \bm J \bm\cdot \grad\dfrac{\ve}{\sigma}$.

  • 线性均匀导电媒质的内部，在达到稳恒状态之前有

    • $-{\displaystyle \frac{\partial \rho }{\partial t}=\mathbf{\nabla }\mathbf{\cdot }\mathit{J}=\sigma \mathbf{\nabla }\mathbf{\cdot }\mathit{E}={\displaystyle \frac{\sigma }{\epsilon }}\rho }$$-\dpdv{\rho}{t} = \div \bm J = \sigma \div \bm E = \dfrac{\sigma}{\ve} \rho$.

    • $\rho ={\rho }_0{\mathrm{e}}^{-\frac{\sigma }{\epsilon }t}={\rho }_0{\mathrm{e}}^{-\frac{t}{\tau }}\to 0$$\rho = \rho_0 \e^{-\tfrac{\sigma}{\ve}t} = \rho_0 \e^{-\tfrac{t}{\tau}} \to 0$.

  • 分界面的自由面电荷

    • ${\rho }_{\text{s}}=D_{\text{1n}}-D_{\text{2n}}=({\displaystyle \frac{{\epsilon }_1}{{\sigma }_1}}-{\displaystyle \frac{{\epsilon }_2}{{\sigma }_2}})J$$\rho_\text s = D_\text{1n} - D_\text{2n} = \pqty{\dfrac{\ve_1}{\sigma_1} - \dfrac{\ve_2}{\sigma_2}} J$.

    • 非理想介质分界面的自由面电荷一般非零.

2.6.4 静电场比拟法与电导

• 双导体的电容与电导

  • $C={\displaystyle \frac{q}{U}}={\displaystyle \frac{{\int }_S\mathit{D}\cdot \mathrm{d}\mathit{S}}{U}}={\displaystyle \frac{\epsilon {\int }_S\mathit{E}\cdot \mathrm{d}\mathit{S}}{U}}$$C = \dfrac{q}{U} = \dfrac{ \int_S \bm D \cdot \dd{\bm S} }{U} = \dfrac{ \ve \int_S \bm E \cdot \dd{\bm S} }{U}$.

  • $G={\displaystyle \frac{I}{U}}={\displaystyle \frac{{\int }_S\mathit{J}\cdot \mathrm{d}\mathit{S}}{U}}={\displaystyle \frac{\sigma {\int }_S\mathit{E}\cdot \mathrm{d}\mathit{S}}{U}}$$G = \dfrac{I}{U} = \dfrac{ \int_S \bm J \cdot \dd{\bm S} }{U} = \dfrac{ \sigma \int_S \bm E \cdot \dd{\bm S} }{U}$.

  • $CR={\displaystyle \frac{C}{G}}={\displaystyle \frac{q}{I}}(={\displaystyle \frac{\mathrm{d}\ln I}{\mathrm{d}t}})={\displaystyle \frac{\epsilon }{\sigma }}$$CR = \dfrac{C}{G} = \dfrac{q}{I} \pqty{= \ddv{\ln I}{t}} = \dfrac{\ve}{\sigma}$.

• 接地电阻的国标为 $\le 4\mathrm{\Omega }$$\le 4 \Omega$.

2.6.5 损耗功率与焦耳定律

损耗功率密度为 $p={\displaystyle \frac{\mathrm{d}P}{\mathrm{d}V}}$$p = \ddv{P}{V}$，焦耳定律为：

• 微分形式：$p=\mathit{J}\mathbf{\cdot }\mathit{E}=\sigma E^2={\displaystyle \frac{J^2}{\sigma }}$$p = \bm J \bm\cdot \bm E = \sigma E^2 = \dfrac{J^2}{\sigma}$.

• 积分形式：$P={\displaystyle {\int }_{V}p\mathrm{d}V=UI}$$P = \dint_V p \dd{V} = UI$.