作业

第 1 章 选频回路与阻抗变换

1-1

对于并联谐振回路，

令 $S={10}^{-16/20}\approx 0.1585$$S = 10^{-16/20} \approx 0.1585$，代入 $f_0=640\mathrm{kHz},\mathrm{\Delta }f=100\mathrm{kHz}$$f_0 = 640\ \rm{kHz}, \Delta f = 100\ \rm{kHz}$，得

于是 ${\mathrm{BW}}_{3\mathrm{dB}}={\displaystyle \frac{f_0}{Q}}\approx 32.1036\mathrm{kHz}$$\rm{BW_{3dB}} = \dfrac{f_0}{Q} \approx 32.1036\ \rm{kHz}$.

1-2

首先有 $Q={\displaystyle \frac{f_0}{{\mathrm{BW}}_{3\mathrm{dB}}}}=66.67$$Q = \dfrac{f_0}{\rm{BW_{3dB}}} = 66.67$，并且 $X_C={\displaystyle \frac{1}{2\pi f_{0}C}}=284.205\mathrm{\Omega }$$X_C = \dfrac{1}{2\pi f_0 C} = 284.205\ \rm{\Omega}$，

于是 $R=X_{C}Q=18.947\mathrm{k}\mathrm{\Omega }$$R = X_C Q = 18.947\ \rm{k\Omega}$，并且 $L={\displaystyle \frac{X_C}{2\pi f_0}}=4.52327\mu \mathrm{H}$$L = \dfrac{X_C}{2\pi f_0} = 4.52327 \rm{\mu H}$.

从而 $S={[1+{\left(Q{\displaystyle \frac{2\mathrm{\Delta }f}{f_0}}\right)}^2]}^{-\frac{1}{2}}=0.124035=-18.1291\mathrm{dB}$$S = \bqty{1 + \pqty{Q \dfrac{2\Delta f}{f_0}}^2}^{-\tfrac{1}{2}} = 0.124035 = -18.1291\ \rm{dB}$.

欲使通带增至 300 kHz，需要 $Q_2={\displaystyle \frac{f_0}{{\mathrm{BW}}_{3\mathrm{dB}}}}=33.33$$Q_2 = \dfrac{f_0}{\rm{BW_{3dB}}} = 33.33$，

于是 $R_2=X_C{Q}_2={\displaystyle \frac{R}{2}}$$R_2 = X_C Q_2 = \dfrac{R}{2}$，从而需要并联 $R_{\text{P}}=R=18.947\mathrm{k}\mathrm{\Omega }$$R_\text P = R = 18.947\ \rm{k\Omega}$.

备注 以后约等于简写为等于.

1-5

由实际并联回路的谐振频率公式，

于是 $r={\displaystyle \frac{2\pi f_{0}L}{Q_0}}=11.4012\mathrm{\Omega }$$r = \dfrac{2\pi f_0 L}{Q_0} = 11.4012\ \rm{\Omega}$，从而 $R_{\text{P}}=(1+Q_0^2)r=114.023\mathrm{k}\mathrm{\Omega }$$R_\text P = (1 +Q_0^2) r = 114.023\ \rm{k\Omega}$，

考虑源电阻与负载电阻，

于是通频带为 ${\mathrm{BW}}_{0.3\mathrm{dB}}={\displaystyle \frac{f_0}{Q_{\mathrm{e}}}}=12.6105\mathrm{kHz}$$\rm{BW_{0.3dB}} = \dfrac{f_0}{Q_\e} = 12.6105\ \rm{kHz}$，

从而选择性为 $S={[1+{\left(Q_{\mathrm{e}}{\displaystyle \frac{2\mathrm{\Delta }f}{f_0}}\right)}^2]}^{-\frac{1}{2}}=0.533354=-5.45969\mathrm{dB}$$S = \bqty{1 + \pqty{Q_\e \dfrac{2\Delta f}{f_0}}^2}^{-\tfrac{1}{2}} = 0.533354 = -5.45969\ \rm{dB}$.

1-6

首先计算 $R_{\text{P}}={\displaystyle \frac{Q_0}{2\pi f_{0}C}}=15.9155\mathrm{k}\mathrm{\Omega }$$R_\text P = \dfrac{Q_0}{2\pi f_0 C} = 15.9155\ \rm{k\Omega}$，于是 $P_2=\sqrt{{\displaystyle \frac{R_{\text{L}}}{R_{\text{P}}}}+{\displaystyle \frac{R_{\text{L}}}{R_{\text{S}}}}{P}_1^2}=0.335905$$P_2 = \sqrt{\dfrac{R_\text L}{R_\text P} + \dfrac{R_\text L}{R_\text S} P_1^2} = 0.335905$，

考虑源电阻与负载电阻，

从而通频带为 ${\mathrm{BW}}_{0.3\mathrm{dB}}={\displaystyle \frac{f_0}{Q_{\mathrm{e}}}}=359.155\mathrm{kHz}$$\rm{BW_{0.3dB}} = \dfrac{f_0}{Q_\e} = 359.155\ \rm{kHz}$.

1-8

由于部分接入的阻抗变换网络 Q 值较高，

回路的总电容为 $C_{\sum }=C_{\mathrm{i}}+{\displaystyle \frac{C_1(C_2+C_0)}{C_1+(C_2+C_0)}}=18.33\mathrm{pF}$$C_\sum = C_\i + \dfrac{C_1 (C_2 + C_0)}{C_1 + (C_2 + C_0)} = 18.33\ \rm{pF}$，

于是 ${\omega }_0={\displaystyle \frac{1}{\sqrt{L{C}_{\sum }}}}=26.1116\mathrm{rad}/\mathrm{s}$$\omega_0 = \dfrac{1}{\sqrt{L C_\sum}} = 26.1116\ \rm{rad/s}$，

从而空载谐振阻抗 $R_{\text{P}}={\omega }_{0}L{Q}_0=20.8893\mathrm{k}\mathrm{\Omega }$$R_\text P = \omega_0 L Q_0 = 20.8893\ \rm{k\Omega}$，

电容部分接入的接入系数为 $P={\displaystyle \frac{C_1}{C_1+C_2+C_0}}={\displaystyle \frac{1}{3}}$$P = \dfrac{C_1}{C_1 + C_2 + C_0} = \dfrac{1}{3}$，

部分接入转全接入，有 $R_0^{\prime }={\displaystyle \frac{R_0}{P^2}}=9R_0$$R'_0 = \dfrac{R_0}{P^2} = 9 R_0$，

于是有载品质因数为

从而通频带为 ${\mathrm{BW}}_{0.3\mathrm{dB}}={\displaystyle \frac{f_0}{Q_{\mathrm{e}}}}=1.47661\mathrm{MHz}$$\rm{BW_{0.3 dB}} = \dfrac{f_0}{Q_\e} = 1.47661\ \rm{MHz}$.

备注 感觉题目中画了并联电阻 $R_{\text{P}}$$R_\text P$. 或者，我的理解是电感有损，等效于并联了电阻 $R_{\mathrm{P}}$$R_\rm P$.

1-9

并联谐振的 Q 值为 $Q_{\mathrm{e}}={\displaystyle \frac{f_0}{{\mathrm{BW}}_{3\mathrm{dB}}}}=10$$Q_\e = \dfrac{f_0}{\rm{BW_{3 dB}}} = 10$，

由于为最大功率传输，并且线圈 Q₀ 视为无穷，

有 $P^2={\displaystyle \frac{R_{\text{L}}}{R_{\text{L}}^{\prime }}}={\displaystyle \frac{R_{\text{L}}}{R_{\text{S}}}}={\displaystyle \frac{1}{9}}$$P^2 = \dfrac{R_\text L}{R_\text L'} = \dfrac{R_\text L}{R_\text S} = \dfrac{1}{9}$，从而 $C_2=2C_1$$C_2 = 2 C_1$，

并且等效总电阻 $R=R_{\text{S}}//R_{\text{L}}^{\prime }=4.5\mathrm{k}\mathrm{\Omega }$$R = R_\text S \parallel R'_\text L= 4.5\ \rm{k\Omega}$，

于是电容为 $L={\displaystyle \frac{R}{{\omega }_0{Q}_{\mathrm{e}}}}={\displaystyle \frac{R}{2\pi f_0{Q}_{\mathrm{e}}}}=4.47623\mu \mathrm{H}$$L = \dfrac{R}{\omega_0 Q_\e} = \dfrac{R}{2\pi f_0 Q_\e} = 4.47623\ \rm{\mu H}$，

从而 $C_{\sum }={\displaystyle \frac{1}{{\omega }_0{X}_{C_{\sum }}}}={\displaystyle \frac{1}{{\omega }_0^{2}L}}=22.1049\mathrm{pF}$$C_\sum = \dfrac{1}{\omega_0 X_{C_\sum}} = \dfrac{1}{\omega_0^2 L} = 22.1049\ \rm{pF}$，

由 $C_{\sum }={\displaystyle \frac{C_1{C}_2}{C_1+C_2}}$$C_\sum = \dfrac{C_1 C_2}{C_1 + C_2}$ 和 $C_2=2C_1$$C_2 = 2 C_1$ 解得 $C_1=33.1573\mathrm{pF},C_2=6.63146\mathrm{pF}$$C_1 = 33.1573\ \rm{pF}, C_2 = 6.63146\ \rm{pF}$.

1-10

并联谐振的 Q 值为 $Q_1={\displaystyle \frac{f_0}{{\mathrm{BW}}_{3\mathrm{dB}}}}=40$$Q_1 = \dfrac{f_0}{\rm{BW_{3 dB}}} = 40$，

角频率 ${\omega }_0=2\pi f_0=6.28319\cdot {10}^9\mathrm{rad}/\mathrm{s}$$\omega_0 = 2 \pi f_0 = 6.28319 \cdot 10^9\ \rm{rad/s}$，

于是并联电感为 $L={\displaystyle \frac{R_{\mathrm{i}}}{{\omega }_0{Q}_1}}=198.944\mathrm{pH}$$L = \dfrac{R_\i}{\omega_0 Q_1} = 198.944\ \rm{pH}$，

并且总电容值为 $C_{\sum }={\displaystyle \frac{1}{{\omega }_0^{2}L}}=127.324\mathrm{pF}$$C_\sum = \dfrac{1}{\omega_0^2 L} = 127.324\ \rm{pF}$.

记并联回路的 Q 值为 $Q_2={\omega }_0{C}_2{R}_2$$Q_2 = \omega_0 C_2 R_2$，则

解得 $Q_2=12.6135$$Q_2 = 12.6135$，从而 $C_2={\displaystyle \frac{Q_2}{{\omega }_0{R}_2}}=401.5\mathrm{pF}$$C_2 = \dfrac{Q_2}{\omega_0 R_2} = 401.5\ \rm{pF}$，

于是 $C_{\text{2S}}={\displaystyle \frac{Q_2^2{C}_2}{1+Q_2^2}}=398.992\mathrm{pF}$$C_\text{2S} = \dfrac{Q_2^2 C_2}{1 + Q_2^2} = 398.992\ \rm{pF}$，由 $C_{\sum }={\displaystyle \frac{C_{\text{2S}}{C}_1}{C_{\text{2S}}+C_1}}$$C_\sum = \dfrac{C_\text{2S} C_1}{C_\text{2S} + C_1}$ 解得 $C_1=186.998\mathrm{pF}$$C_1 = 186.998\ \rm{pF}$.

1-12

由于输入阻抗大于负载电阻，若采取 L 网络阻抗变换，则负载电阻与匹配网络中的电感串联，刚好可以与寄生电感合并，因此这里采用 L 网络阻抗变换。

大致思路如下图所示，负载与电感串联后变换为并联，从而增大负载电阻；而为了使输入阻抗为纯电阻，还需要并联电容。

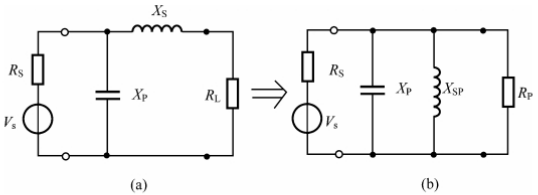
由输入阻抗 $R_{\mathrm{i}}=R_{\text{P}}=(1+Q^2)R_{\text{L}}$$R_\i = R_\text P = (1 + Q^2) R_\text L$，解得并联回路的品质因数为 $Q=2$$Q = 2$.

于是根据品质因数的定义式 $Q={\displaystyle \frac{X_{\text{S}}}{R_{\text{L}}}}={\displaystyle \frac{R_{\text{P}}}{X_{\text{P}}}}$$Q = \dfrac{X_\text S}{R_\text L} = \dfrac{R_\text P}{X_\text{P}}$，解得 $C_{\text{P}}=63.662\mathrm{pF}$$C_\text{P} = 63.662\ \rm{pF}$，

串联总阻抗为 $X_{\text{S}}=20\mathrm{\Omega }$$X_\text{S} = 20\ \Omega$，减去原有的阻抗，有 $X_S^{\prime }=X_S-{\omega }_0{L}_0=-42.8319\mathrm{\Omega }$$X_S' = X_S - \omega_0 L_0 = -42.8319\ \Omega$，

因此需要新串联的元件为电容而非电感，其参数为 $C_{\text{S}}=-{\displaystyle \frac{1}{{\omega }_0{X}_{\text{S}}^{\prime }}}=37.1581\mathrm{pF}$$C_\text S = -\dfrac{1}{\omega_0 X'_\text S} = 37.1581\ \rm{pF}$.

1-14

什么是归一化阻抗变换？如果取 $Z_{\mathrm{L}}=50z_{\mathrm{L}}$$Z_\rm L = 50 z_\rm L$ 的话：

（1）$z_{\text{L}}=(0.5-\mathrm{j}0.8)\mathrm{\Omega }$$z_\text L = (0.5 - \j 0.8)\ \Omega$.

$Z_{\text{L}}=50z_{\text{L}}=(25-\mathrm{j}40)\mathrm{\Omega }$$Z_\text L = 50 z_\text L = (25 - \j 40)\ \Omega$，于是内接电感，且 $Q=\sqrt{{\displaystyle \frac{50}{25}}-1}=1$$Q = \sqrt{\dfrac{50}{25} - 1} = 1$，

从而串联电感 $X_{\text{L}}=R_{\text{L}}Q+X_{C_L}=65\mathrm{\Omega }$$X_\text L = R_\text L Q + X_{C_L} = 65\ \Omega$，并联电容 $X_C={\displaystyle \frac{R_{\text{S}}}{Q}}=50\mathrm{\Omega }$$X_C = \dfrac{R_\text S}{Q} = 50\ \Omega$.

（2）$z_{\text{L}}=(1.6+\mathrm{j}0.8)\mathrm{\Omega }$$z_\text L = (1.6 + \j 0.8)\ \Omega$.

$Z_{\text{L}}=50z_{\text{L}}=(80+\mathrm{j}40)\mathrm{\Omega }$$Z_\text L = 50 z_\text L = (80 + \j 40)\ \Omega$，于是外接电感，且 $Q=\sqrt{{\displaystyle \frac{80}{50}}-1}=0.774$$Q = \sqrt{\dfrac{80}{50} - 1} = 0.774$，

先用串联电容 $X_{C_1}=40\mathrm{\Omega }$$X_{C_1} = 40\ \Omega$ 抵消负载感抗，

再并联电容 $X_C={\displaystyle \frac{R_{\text{L}}}{Q}}=103.3\mathrm{\Omega }$$X_C = \dfrac{R_\text L}{Q} = 103.3\ \Omega$ 实现阻抗变换，

最后串联 $X_L=R_{\text{S}}Q=38.7\mathrm{\Omega }$$X_L = R_\text S Q= 38.7\ \Omega$ 从而使输入阻抗为纯电阻.

第 2 章 噪声与非线性变换

2-1^*

（1）

$\overline{I_{\text{n}}^2}={\displaystyle \frac{4kTB}{R}}=3.13882\times {10}^{-21}{\mathrm{A}}^2$$\overline{I_\text n^2} = \dfrac{4 k T B}{R} = 3.13882 \cp 10^{-21}\ \rm{A^2}$.

$\overline{V_{\text{n}}^2}=\overline{I_{\text{n}}^2}{R}^2=8.16408\times {10}^{-10}{\mathrm{V}}^2$$\overline{V_\text n^2} = \overline{I_\text n^2} R^2 = 8.16408 \cp 10^{-10}\ \rm V^2$.

（2）

$\overline{V_{\text{n}}^2}=4kTB(R_1//R_2)=2.68555{\mathrm{V}}^2$$\overline{V_\text n^2} = 4 k T B (R_1 \parallel R_2) = 2.68555\ \rm{V^2}$.

2-2^*

$P_{\text{n}}={\displaystyle \frac{4kTB}{R_1+R_2}}{\displaystyle \frac{1}{4}}(R_1+R_2)=kTB$$P_\text n = \dfrac{4k T B}{R_1 + R_2} \dfrac{1}{4} (R_1 + R_2) = k T B$.

2-3

⭐️

$H(\omega )={\displaystyle \frac{1}{1+\mathrm{j}\omega RC}}$$H(\omega) = \dfrac{1}{1 + \j\omega R C}$,

$N_0=n_0{\displaystyle {\int }_0^{+\mathrm{\infty }}{|H(\omega )|}^2\mathrm{d}f=n_0{\displaystyle {\int }_0^{+\mathrm{\infty }}{\displaystyle \frac{\mathrm{d}f}{1+4{\pi }^2{f}^2{R}^2{C}^2}}={\displaystyle \frac{n_0}{2\pi RC}}\cdot {\displaystyle \frac{\pi }{2}}={\displaystyle \frac{n_0}{4RC}}}}$$N_0 = n_0 \intoi \vqty{H(\omega)}^2 \dd{f} = n_0 \intoi \dfrac{\dd{f}}{1 + 4\pi^2 f^2 R^2 C^2} = \dfrac{n_0}{2\pi RC} \cdot \dfrac{\pi}{2} = \dfrac{n_0}{4 RC}$.

2-4

$T_{\mathrm{e}1}=(F_1-1)T_0=288.626\mathrm{K}$$T_{\e1} = (F_1 - 1) T_0 = 288.626\ \rm K$,

$T_{\mathrm{e}}=T_{\mathrm{e}1}+{\displaystyle \frac{T_{\mathrm{e}2}}{G_{\text{P1}}}}=313.924\mathrm{K}$$T_\e = T_{\e1} + \dfrac{T_{\e2}}{G_\text{P1}} = 313.924\ \rm K$.

$F=1+{\displaystyle \frac{T_{\mathrm{e}}}{T_0}}=2.0825$$F = 1 + \dfrac{T_\e}{T_0} = 2.0825$.

2-5

$F_{\text{t}}=k[T_{\text{a}}+(F-1)T_0]B=-174\mathrm{dBm}/\mathrm{Hz}+3\mathrm{dB}+10\lg B=121\mathrm{dBm}$$F_\text t = k \bqty{T_\text a + (F - 1) T_0} B = -174\ \rm{dBm / Hz} + 3\rm{dB} + 10\lg B = 121\ \rm{dBm}$,

$P_{\text{in, min}}=F_t(\mathrm{SNR}{)}_{0,\min }=-101\mathrm{dBm}$$P_\text{in, min} = F_t \rm{(SNR)_{0, min}} = -101\ \rm{dBm}$,

${\mathrm{DR}}_{\mathrm{l}}=-10\mathrm{dBm}-P_{\text{in, min}}=91\mathrm{dBm}$$\rm{DR_l} = -10\rm{dBm} - P_\text{in, min} = 91\rm{dBm}$.

2-6^*

$H(\omega )={\displaystyle \frac{1}{\mathrm{j}(\omega C-\frac{1}{\omega L})+\frac{1}{R}}}$$H(\omega) = \dfrac{1}{\j (\omega C - \cfrac{1}{\omega L}) + \cfrac{1}{R}}$，$H({\omega }_0)=R$$H(\omega_0) = R$,

${\displaystyle {\int }_0^{+\mathrm{\infty }}|H(\omega )|\mathrm{d}f=}$$\intoi \vqty{H(\omega)} \dd{f} =$,

备注 $B_{\text{L}}={\displaystyle \frac{1}{4RC}}$$B_\text L = \dfrac{1}{4 RC}$. 🌙

2-7

⭐️

（1）线性动态范围

$F_{\text{t}}=k(T_{\text{a}}+(F-1)T_0)B=-87.4161\mathrm{dBm}$$F_\text t = k (T_\text a + (F - 1) T_0) B = -87.4161\ \rm{dBm}$,

$P_{\text{i, 1dB}}=25-39=-14\mathrm{dBm}$$P_\text{i, 1dB} = 25 - 39 = -14\ \rm{dBm}$,

以基底噪声为下限：${\mathrm{DR}}_{\mathrm{l}}=73.4171\mathrm{dB}$$\rm{DR_l} = 73.4171\ \rm{dB}$.

以灵敏度为下限：${\mathrm{DR}}_{\mathrm{l}}=63.4171\mathrm{dB}$$\rm{DR_l} = 63.4171\ \rm{dB}$.

（2）无杂散动态范围

${\mathrm{IIP}}_3={\mathrm{OIP}}_3-G=-5\mathrm{dBm}$$\rm{IIP_3} = \rm{OIP}_3 - G = -5\ \rm{dBm}$,

以基底噪声为下限：${\mathrm{DR}}_{\mathrm{f}}=54.9447\mathrm{dB}$$\rm{DR_f} = 54.9447\ \rm{dB}$.

以灵敏度为下限：${\mathrm{DR}}_{\mathrm{f}}=44.9447\mathrm{dB}$$\rm{DR_f} = 44.9447\ \rm{dB}$.

2-8

${\displaystyle \text{OIP3}=\frac{{10}^{14/10.}}{\frac{100}{{10}^{22/10}}+\frac{100}{{10}^{13/10}}}=6.48503}$$\d \text{OIP3}=\frac{10^{14/10.}}{\frac{100}{10^{22/10}}+\frac{100}{10^{13/10}}} = 6.48503$,

2-9

与 2-8 同理得 20.8067 dBm.

2-12

$P_{\text{in, min}}=k(T_{\text{a}}+(F-1)T_0)B(\mathrm{SNR}{)}_{\mathrm{i}}=-108.053\mathrm{dBm}$$P_\text{in, min} = k (T_\text a + (F - 1) T_0) B \rm{(SNR)_\i} = -108.053\ \rm{dBm}$.

$V_{\text{in}}=\sqrt{R_{\text{in}}{P}_{\text{in, min}}}=8.84761\ast {10}^{-5}\mathrm{V}$$V_\text{in} = \sqrt{R_\text{in} P_\text{in, min}} = 8.84761 * 10^{-5}\ \rm V$.

$A_{\text{V}}=115.043\mathrm{dB}$$A_\text V = 115.043\ \rm{dB}$.

2-13

$F=F_1+{\displaystyle \frac{F_2-1}{G_{\text{PA1}}}}=13.861=11.4186\mathrm{dB}$$F = F_1 + \dfrac{F_2 - 1}{G_\text{PA1}} = 13.861 = 11.4186\ \rm{dB}$,

1. $P_{\text{in, min}}=-117.787\mathrm{dB}$$P_\text{in, min} = -117.787\ \rm{dB}$,

2. $P_{\text{in, min}}=-115.55\mathrm{dB}$$P_\text{in, min} = -115.55\ \rm{dB}$.

第 3 章 调制和解调

3-1

⭐️

进行了两次 AM 调制，第一次将 $F=3\mathrm{kHz}$$F = 3\ \rm{kHz}$ 的音频调制到载频 $f_1=10\mathrm{kHz}$$f_1 = 10\ \rm{kHz}$ 和 $f_2=30\mathrm{kHz}$$f_2 = 30\ \rm{kHz}$ 上，第二次再将其调制到主载频 $f_0=1000\mathrm{kHz}$$f_0 = 1000\ \rm{kHz}$ 上.

平均功率为

${\mathrm{BW}}_{\mathrm{AM}}=66\mathrm{kHz}$$\rm{BW_AM} = 66\ \rm{kHz}$.

3-2

1. $P_{\text{c}}={\displaystyle \frac{{10}^2}{2}}\mathrm{mW}=50\mathrm{mW}$$P_\text c = \dfrac{10^2}{2}\ \rm{mW} = 50\ \rm{mW}$.

2. $P={\displaystyle \frac{5^2}{4}}\mathrm{mW}=6.25\mathrm{mW}$$P = \dfrac{5^2}{4}\ \rm{mW} = 6.25\ \rm{mW}$.

3. $P_{max}={\displaystyle \frac{{10}^2}{2}}(1+0.5{)}^2=112.5\mathrm{mW}$$P_\max = \dfrac{10^2}{2} (1 + 0.5)^2 = 112.5\ \rm{mW}$.

4. $P_{min}={\displaystyle \frac{{10}^2}{2}}(1-0.5{)}^2=12.5\mathrm{mW}$$P_\min = \dfrac{10^2}{2} (1 - 0.5)^2 = 12.5\ \rm{mW}$.

3-6

1. 信号：

   $$\begin{array}{rl}{v}_{\text{1}}(t)& =A{V}_{\mathrm{AM}}(1+m_1\cos {\mathrm{\Omega }}_{1}t+m_2\cos {\mathrm{\Omega }}_{2}t)\cos {\omega }_{\text{c}}t,\\ v_2(t)& =0.1A{V}_{\mathrm{AM}}\cos {\omega }_{\text{c}}t+0.5A{V}_{\mathrm{AM}}{m}_1\cos ({\omega }_{\text{c}}+{\mathrm{\Omega }}_1)t+0.5A{V}_{\mathrm{AM}}{m}_2\cos ({\omega }_{\text{c}}+{\mathrm{\Omega }}_2)t,\\ v_3(t)& =0.1A{V}_{\mathrm{AM}}{m}_1\cos ({\omega }_{\text{c}}-{\mathrm{\Omega }}_1)t+0.5A{V}_{\mathrm{AM}}\cos \left({\omega }_{\text{c}}t\right)+\\ & 0.4A{V}_{\mathrm{AM}}{m}_1\cos ({\omega }_{\text{c}}+{\mathrm{\Omega }}_1)t+0.5A{V}_{\mathrm{AM}}{m}_2\cos ({\omega }_{\text{c}}+{\mathrm{\Omega }}_2)t.\end{array}$$

2. 双边调制（AM）；单边带信号（SSB）；残留边带调幅.

3. 包络检波或相干解调；相干解调（同步检波）；相干解调.

3-9

调频（FM）：相位为角频率的积分.

调相（AM）：角频率为相位的导数.

3-11

1. $v(t)=30\cos (18\pi \times {10}^{7}t+5\sin (4\pi \times {10}^{4}t))$$v(t) = 30 \cos(18\pi \cp 10^7 t + 5 \sin(4\pi \cp 10^4 t))$.

2. $\mathrm{\Delta }{f}_{\text{m}}=m_{\text{f}}F=100\mathrm{kHz}$$\Delta f_\text m = m_\text f F = 100\ \rm{kHz}$.

3. ${\mathrm{BW}}_{\mathrm{CR}}=2(\mathrm{\Delta }{f}_{\text{m}}+F)=240\mathrm{kHz}$$\rm{BW_CR} = 2 (\Delta f_\text m + F) = 240\ \rm{kHz}$.

4. $P={\displaystyle \frac{{30}^2}{2\cdot 50}}=9\mathrm{W}$$P = \dfrac{30^2}{2 \cdot 50} = 9\ \rm W$.

5. $P_{\mathrm{o}}={|J_0(5)|}^2=0.04$$P_\o = \vqty{J_0(5)}^2 = 0.04$.

3-12

🌙

1. $\mathrm{\Delta }{f}_{\text{m}}=m_{\text{f}}F\Rightarrow m_{\text{f}}=3$$\Delta f_\text m = m_\text f F \RA m_\text f = 3$,

   $\omega (t)=2\pi \times 50\times {10}^6+2\pi \times 6\times {10}^3\cos 2\pi \times 2\times {10}^{3}t\mathrm{rad}/\mathrm{s}$$\omega(t) = 2\pi \cp 50 \cp 10^6 + 2\pi \cp 6 \cp 10^3 \cos 2\pi \cp 2 \cp 10^3 t\ \rm{rad / s}$,

   $\phi (t)={10}^8\pi t+3\sin 4\pi \times {10}^{3}t\mathrm{rad}$$\varphi(t) = 10^8 \pi t + 3 \sin 4\pi \cp 10^3 t\ \rm{rad}$,

   $v(t)=5\cos ({10}^8\pi t+3\sin 4\pi \times {10}^{3}t)\mathrm{V}$$v(t) = 5 \cos(10^8 \pi t + 3 \sin 4\pi \cp 10^3 t)\ \rm V$.

2. $\mathrm{\Delta }{\phi }_{\text{m}}=m_{\text{p}}=4.5$$\Delta \varphi_\text m = m_\text p = 4.5$,

   $\phi (t)={10}^8\pi t+4.5\cos 4\pi \times {10}^{3}t\mathrm{rad}$$\varphi(t) = 10^8\pi t + 4.5 \cos 4\pi \cp 10^3 t\ \rm{rad}$,

   $\omega (t)={10}^8\pi t-18\pi \times {10}^3\sin 4\pi \times {10}^{3}t\mathrm{rad}/\mathrm{s}$$\omega(t) = 10^8\pi t - 18\pi \cp 10^3 \sin 4\pi \cp 10^3 t\ \rm{rad/s}$,

   $v(t)=4\cos ({10}^8\pi t+4.5\cos 4\pi \times {10}^{3}t)\mathrm{V}$$v(t) = 4 \cos(10^8\pi t + 4.5 \cos 4\pi \cp 10^3 t)\ \rm{V}$.

3. （1）1.5 V, 2 kHz

   1. 调频波：$m_{\text{f}}=3,{\mathrm{BW}}_{\mathrm{CR}}=16\mathrm{kHz}$$m_\text f = 3, \rm{BW_CR} = 16\ \rm{kHz}$.

   2. 调相波：$m_{\text{p}}=4.5,{\mathrm{BW}}_{\mathrm{CR}}=22\mathrm{kHz}$$m_\text p = 4.5, \rm{BW_CR} = 22\ \rm{kHz}$.

   （2）1.5 V, 4 kHz

   1. 调频波：1.5, 20 kHz.

   2. 调相波：4.5, 44 kHz.

   （3）3 V, 2 kHz

   1. 调频波：6, 28 kHz.

   2. 调相波：9, 40 kHz.

备注 注意题目中给出了单位电压的频偏，而非最大电压.

3-13

$v(t)=10\cos (4\pi \times {10}^{7}t+3\sin 4\pi \times {10}^{3}t+{\displaystyle \frac{8}{3}}\sin 5\pi \times {10}^{3}t)\mathrm{V}$$v(t) = 10 \cos(4\pi \cp 10^7 t + 3 \sin 4\pi \cp 10^3 t + \dfrac{8}{3} \sin 5\pi \cp 10^3 t)\ \rm V$.

频率：$\omega (t)=4\pi \times {10}^7+12\pi \times {10}^3\cos 4\pi \times {10}^{3}t+{\displaystyle \frac{4}{3}}{10}^4\cos 4\pi \times {10}^{3}t\mathrm{rad}/\mathrm{s}$$\omega(t) = 4\pi \cp 10^7 + 12\pi \cp 10^3 \cos4\pi \cp 10^3 t + \dfrac{4}{3} 10^4 \cos4\pi \cp 10^3 t\ \rm{rad/s}$.

频谱分量的频率略.

第 4 章 发送机接收机结构

4-5

⭐️

1. $(\mathrm{SNR}{)}_{\mathrm{i}}=15\mathrm{dB}$$\rm{(SNR)_i} = 15\ \rm{dB}$.

2. $S_{\mathrm{out}}=-80\mathrm{dBm}$$S_\rm{out} = -80\ \rm{dBm}$.

3. $N_{\text{out}}=Gk(F-1)T_{0}B+G{N}_{\mathrm{i}}=-94.0243\mathrm{dBm}$$N_\text{out} = G k (F - 1) T_0 B + GN_\i = -94.0243\ \rm{dBm}$.

4. $(\mathrm{SNR}{)}_{\mathrm{o}}=14.0243\mathrm{dB}$$\rm{(SNR)_o} = 14.0243\ \rm{dB}$.

4-10

1. 噪声系数：

   $$\begin{array}{rl}F& =F_1+{\displaystyle \frac{F_2-1}{G_{\mathrm{P}1}}}+{\displaystyle \frac{F_3-1}{G_{\mathrm{P}1}{G}_{\mathrm{P}2}}}\\ & ={10}^{2/10}+{\displaystyle \frac{{10}^{1/10}-1}{{10}^{10/10}}}+{\displaystyle \frac{{10}^{4/10}-1}{{10}^{10/10}\cdot {10}^{-1/10}}}\\ & \approx 1.80112\approx 2.55543\mathrm{dB}.\end{array}$$

2. $T_{\mathrm{e}}=(F-1)T_0=232.325\mathrm{K}$$T_\e = (F - 1) T_0 = 232.325\ \rm K$.

3. $N_{\mathrm{o}}=Gk(T_{\mathrm{e}}+T_{\text{a}})B=1.35877\times {10}^{-13}\mathrm{W}=-98.6695\mathrm{dBm}$$N_\o = G k (T_\e + T_\text a) B = 1.35877 \cp 10^{-13}\ \rm{W} = -98.6695\ \rm{dBm}$.

4. $S_{\mathrm{DSB}}={\displaystyle \frac{N_0}{B}}=-168.669\mathrm{dBm}$$S_\rm{DSB} = \dfrac{N_0}{B} = -168.669\ \rm{dBm}$.

5. $V_{\mathrm{in},\min }=\sqrt{{\displaystyle \frac{(\mathrm{SNR}{)}_{\mathrm{o}}{N}_{\mathrm{o}}}{R\cdot G}}}=13.0635\mu \mathrm{V}$$V_\rm{in, min} = \sqrt{\dfrac{\rm{(SNR)_o} N_\o}{R \cdot G}} = 13.0635\ \rm{\mu V}$.

第 5 章 低噪声放大器

5-3

5-4

5-5

5-9

第 6 章 混频器

6-6

由于本振信号幅度较大，近似起到开关作用，即 $i_c(t)=a{[v_{\mathrm{RF}}(t)+v_{\mathrm{LO}}(t)]}^2{S}_1({\omega }_{\mathrm{LO}}t)$$i_c(t) = a \bqty{v_\rm{RF}(t) + v_\rm{LO}(t)}^2 S_1(\omega_\rm{LO} t)$，

其中 $S_1({\omega }_{\mathrm{LO}}t)={\displaystyle \frac{1}{2}}+{\displaystyle \frac{2}{\pi }}\cos \left({\omega }_{\mathrm{LO}}t\right)+\cdots$$S_1(\omega_\rm{LO}t) = \dfrac{1}{2} + \dfrac{2}{\pi} \cos(\omega_\rm{LO} t) + \cdots$，由于平方可以直接得到乘积项，这里只取单向开关函数的直流分量，于是积化和差后得到中频信号 $i_{\mathrm{IF}}(t)={\displaystyle \frac{a}{2}}{V}_{\mathrm{RF}}{V}_{\mathrm{LO}}\cos ({\omega }_{\mathrm{RF}}-{\omega }_{\mathrm{LO}})t$$i_\rm{IF}(t) = \dfrac{a}{2} V_\rm{RF} V_\rm{LO} \cos(\omega_\rm{RF} - \omega_\rm{LO})t$，

从而变频跨导为 $g_{\mathrm{fc}}={\displaystyle \frac{a}{2}}{V}_{\mathrm{LO}}$$g_\rm{fc} = \dfrac{a}{2} V_\rm{LO}$，电压增益为 $A_{\mathrm{V}}={\displaystyle \frac{a}{2}}{V}_{\mathrm{LO}}{R}_{\mathrm{IF}}$$A_\rm V = \dfrac{a}{2} V_\rm{LO} R_\rm{IF}$，其中 $R_{\mathrm{IF}}$$R_\rm{IF}$ 为中频负载电阻.

备注 也可以直接研究时变跨导 $g(t)=2a\cdot v_{\mathrm{LO}}(t)\cdot S_1({\omega }_{\mathrm{LO}}t)$$g(t) = 2a \cdot v_\rm{LO}(t) \cdot S_1(\omega_\rm{LO}t)$.

6-7

1. $V_{\mathrm{Q}}=-{\displaystyle \frac{1}{2}}{V}_{1\mathrm{m}}$$V_\rm Q = -\dfrac{1}{2} V_\rm{1m}$，曲线如下图所示：

   

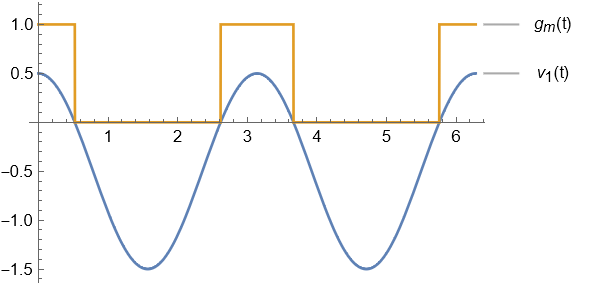
   傅里叶级数略，可参考备注中的代码. 跨导含有基波分量，因此可以实现频谱搬移.

2. $V_{\mathrm{Q}}=0$$V_\rm Q = 0$，此时 $g_{\text{m}}(t)=S_1({\omega }_{1}t)$$g_\text m(t) = S_1(\omega_1 t)$.

   

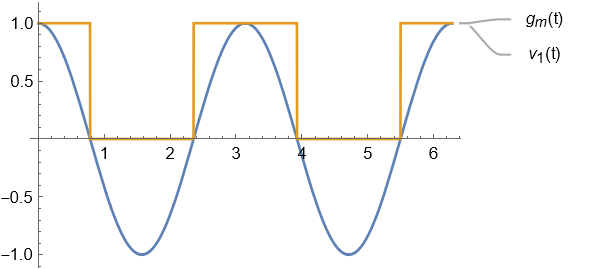
   傅里叶级数见教材 58 页. 跨导含有基波分量，因此可以实现频谱搬移.

3. $V_{\mathrm{Q}}=V_{1\text{m}}$$V_\rm Q = V_{1\text m}$，此时为线性，跨导为常数，因此不能实现频谱搬移功能.

备注

• 考试时应该不会让我们求傅里叶级数，计算繁琐而无实质难度，但是花时间.

• 附 mathematica 代码（在 mathematica 写完复制过来的，懒得整理代码排版了）；原来 mathematica 的绘图标签不按颜色标注，按的是曲线的形状和延伸趋势.

​x
1
(* 1 *)
2
Subscript[\[Omega], 1] = 2; Subscript[V, 1 m] = 1; Subscript[g, D] = 1;
3
Subscript[v, 1][t_] := 
4
  Subscript[V, 1 m] Cos[Subscript[\[Omega], 1] t] - 0.5;
5
Subscript[g, m][t_] := 
6
  Subscript[g, D] HeavisideTheta[Subscript[v, 1][t]];
7
Plot[{Subscript[v, 1][t], Subscript[g, m][t]}, {t, 0, 2 Pi}, 
8
 PlotLabels -> {"\!\(\*SubscriptBox[\(v\), \(1\)]\)(t)", 
9
   "\!\(\*SubscriptBox[\(g\), \(m\)]\)(t)"}]
10

11
Table[FourierCosCoefficient[Subscript[g, m][t], t, n], {n, 0, 4}]
12

13
(* 2 *)
14
Subscript[v, 1][t_] := Subscript[V, 1 m] Cos[Subscript[\[Omega], 1] t];
15
Plot[{Subscript[v, 1][t], Subscript[g, m][t]}, {t, 0, 2 Pi}, 
16
 PlotLabels -> {"\!\(\*SubscriptBox[\(v\), \(1\)]\)(t)", 
17
   "\!\(\*SubscriptBox[\(g\), \(m\)]\)(t)"}]

6-8

（1）混频

当 $v_1$$v_1$ 为大信号、$v_2$$v_2$ 为小信号时，可如题述表达式近似计算.

此时 $v_1(t)$$v_1(t)$ 保证工作在线性时变状态，以产生组合频率分量.

因此取 $v_1(t)=v_{\mathrm{LO}}(t)$$v_1(t) = v_\rm{LO}(t)$（本振大信号），$v_2(t)=v_{\mathrm{RF}}(t)$$v_2(t) = v_\rm{RF}(t)$（射频小信号）.

于是输出电流包含的频率分量有 $|{\omega }_{\mathrm{RF}}\pm (2k+1){\omega }_{\mathrm{LO}}|,k\in \mathbb{N}$$\vqty{\omega_\rm{RF} \pm (2k+1) \omega_\rm{LO}}, k \in \N$.

滤波器的中心频率为 ${\omega }_{\mathrm{IF}}={\omega }_{\mathrm{RF}}-{\omega }_{\mathrm{LO}}$$\omega_\rm{IF} = \omega_\rm{RF} - \omega_\rm{LO}$，带宽为 $2{\omega }_{\mathrm{RF}}$$2 \omega_\rm{RF}$.

（2）双边带调制

与（1）的思路类似，取 $v_1(t)=v_{\text{c}}(t)$$v_1(t) = v_\text c(t)$（载波大信号），$v_2(t)=v_{\mathrm{\Omega }}(t)$$v_2(t) = v_\Omega(t)$（调制小信号）.

于是输出电流包含的频率分量有 $|(2k+1){\omega }_{\mathrm{c}}\pm \mathrm{\Omega }|,k\in \mathbb{N}$$\vqty{(2k + 1) \omega_\rm c \pm \Omega}, k \in \N$.

滤波器的中心频率为 ${\omega }_{\text{c}}$$\omega_\text c$，带宽为 $2\mathrm{\Omega }$$2 \Omega$.

（3）双边带调制波解调

对于频率为 ${\omega }_{\text{c}}+\mathrm{\Omega }$$\omega_\text c + \Omega$ 的已调波，通过频率为 ${\omega }_{\text{r}}={\omega }_{\text{c}}$$\omega_\text r = \omega_\text c$ 的参考信号与之相乘即可.

因此取 $v_1(t)=v_{\text{r}}(t)$$v_1(t) = v_\text r(t)$（参考信号），$v_2(t)=v_{\text{DSB}}(t)$$v_2(t) = v_\text{DSB}(t)$（双边带调制信号）.

于是输出电流包含的频率分量有 $|2k{\omega }_{\text{c}}\pm \mathrm{\Omega }|,k\in \mathbb{N}$$\vqty{2k \omega_\text c \pm \Omega}, k \in \N$.

滤波器为低通滤波器，带宽为 $\mathrm{\Omega }$$\Omega$.

备注 双曲正切函数的泰勒展开式只包含奇次分量，并可用伯努利数表示为

6-9

该电路为单平衡混频器，输出电压由电容滤去直流分量，因此 $v_{\mathrm{o}}(t)$$v_\o(t)$ 即下式的交流分量：

其中

中频频率为 ${\omega }_{\mathrm{IF}}={\omega }_{\mathrm{LO}}-{\omega }_{\mathrm{S}}={10}^7\mathrm{rad}/\mathrm{s}$$\omega_\rm{IF} = \omega_\rm{LO} - \omega_\rm{S} = 10^7\ \rm{rad/s}$, 于是并联回路空载谐振阻抗为

从而等效负载阻抗为

在常温下，取 $U_{\mathrm{T}}={\displaystyle \frac{kT}{q}}=26\mathrm{mV}$$U_\rm T = \dfrac{kT}{q} = 26\ \rm{mV}$，近似取 $\tanh x\approx x$$\tanh x \approx x$，于是有

备注

• 应知道 $300\mathrm{K}$$300\ \rm K$ 时有 $U_{\mathrm{T}}:={\displaystyle \frac{kT}{q}}\approx 26\mathrm{mV}$$U_\rm T := \dfrac{kT}{q} \approx 26\ \rm{mV}$.

• 应当熟悉差分放大电路的输出电流公式，或者知道如何推导.

• 注意图中未画出并联回路的空载谐振阻抗，我的理解是电感 L 有损，可等效为并联电阻 $R_{\mathrm{P}}$$R_\rm P$.

6-14

1. 由于本振信号可作为开关函数，当二极管导通时，有下左式：

   $$\{\begin{array}{l}{v}_{\mathrm{L}}(t)+v_{\mathrm{S}}(t)-i_{{\mathrm{D}}_1}(t)R_{\mathrm{D}}=v_{\mathrm{o}}(t),\\ v_{\mathrm{L}}(t)-v_{\mathrm{S}}(t)-i_{{\mathrm{D}}_2}(t)R_{\mathrm{D}}=-v_{\mathrm{o}}(t),\\ v_{\mathrm{o}}(t)=(i_{{\mathrm{D}}_1}(t)-i_{{\mathrm{D}}_2}(t))R_{\mathrm{L}}.\end{array}\Rightarrow v_{\mathrm{o}}(t)={\displaystyle \frac{2R_{\mathrm{L}}}{2R_{\mathrm{L}}+R_{\mathrm{D}}}}{v}_{\mathrm{S}}(t)S_1({\omega }_{\mathrm{L}}t).$$

2. 当 $v_{\mathrm{L}}(t)>0$$v_\rm L(t) > 0$ 时，可认为二极管都导通，反之则都截止. 于是有

   $$\{\begin{array}{l}{v}_{\mathrm{S}}(t)+v_{\mathrm{L}}(t)-v_{\mathrm{o}}(t)=i_{D_1}(t)R_{\mathrm{D}},\\ v_{\mathrm{S}}(t)-v_{\mathrm{L}}(t)-v_{\mathrm{o}}(t)=-i_{{\mathrm{D}}_2}(t)R_{\mathit{D}},\\ v_{\mathrm{o}}(t)=(i_{{\mathrm{D}}_1}(t)-i_{{\mathrm{D}}_2}(t))R_{\mathrm{L}}.\end{array}\Rightarrow v_{\mathrm{o}}(t)={\displaystyle \frac{2R_{\mathrm{L}}}{2R_{\mathrm{L}}+R_{\mathrm{D}}}}{v}_{\mathrm{S}}(t)S_1({\omega }_{\mathrm{O}}t).$$

3. 当 $v_{\mathrm{L}}(t)>0$$v_\rm L(t) > 0$ 时，$v_{\mathrm{L}}(t)+v_{\mathrm{S}}(t)-v_{\mathrm{o}}(t)=i_{{\mathrm{D}}_1}(t)R_{\mathrm{D}}$$v_\rm L(t) + v_\rm S(t) - v_\o(t) = i_\rm{D_1}(t) R_\rm D$,

   当 $v_{\mathrm{L}}(t)<0$$v_\rm L(t) < 0$ 时，$v_{\mathrm{L}}(t)-v_{\mathrm{S}}(t)-v_{\mathrm{o}}(t)=-i_{{\mathrm{D}}_2}(t)R_{\mathrm{D}}$$v_\rm L(t) - v_\rm S(t) - v_\o(t) = -i_\rm{D_2}(t) R_\rm D$.

   其中 $v_{\mathrm{o}}(t)=(i_{{\mathrm{D}}_1}(t)-i_{{\mathrm{D}}_2}(t))R_{\mathrm{L}}$$v_\o(t) = (i_\rm{D_1}(t) - i_\rm{D_2}(t)) R_\rm L$，于是

   $$v_{\mathrm{o}}(t)={\displaystyle \frac{R_{\mathrm{L}}}{R_{\mathrm{L}}+R_{\mathrm{D}}}}[v_{\mathrm{S}}(t)S_2({\omega }_{\mathrm{L}}t)+v_{\mathrm{L}}].$$

注意 第一问涉及到多个变压器，需要列写回路方程，而不能直接使用单个变压器的阻抗变换公式.

6-15

同 6-15.1 分析可知，

于是中频电流为 $i_{\mathrm{IF}}={\displaystyle \frac{V_{\mathrm{Sm}}}{\pi R_{\mathrm{L}}}}\cos ({\omega }_{\mathrm{L}}-{\omega }_{\mathrm{S}})t$$i_\rm{IF} = \dfrac{V_\rm{Sm}}{\pi R_\rm L} \cos(\omega_\rm{L} - \omega_\rm S) t$，

中频功率为 $P_{\mathrm{IF}}={\displaystyle \frac{V_{\mathrm{Sm}}^2}{2{\pi }^2{R}_{\mathrm{L}}}}$$P_\rm{IF} = \dfrac{V_\rm{Sm}^2}{2\pi^2 R_\rm L}$.

输入端射频信号电流分量为：$i_{\mathrm{S}}={\displaystyle \frac{V_{\mathrm{Sm}}}{2R_{\mathrm{L}}}}\cos \left({\omega }_{\mathrm{L}}t\right)$$i_\rm{S} = \dfrac{V_\rm{Sm}}{2 R_\rm L} \cos(\omega_\rm L t)$，

于是射频信号功率为 $P_{\mathrm{RF}}={\displaystyle \frac{V_{\mathrm{Sm}}^2}{4R_{\mathrm{L}}}}$$P_\rm{RF} = \dfrac{V_\rm{Sm}^2}{4 R_\rm L}$，

从而变频损耗为 $L_{\mathrm{M}}={\displaystyle \frac{P_{\mathrm{RF}}}{P_{\mathrm{IF}}}}={\displaystyle \frac{{\pi }^2}{2}}\approx 6.9327\mathrm{dB}$$L_\rm M = \dfrac{P_\rm{RF}}{P_\rm{IF}} = \dfrac{\pi^2}{2} \approx 6.9327\ \rm{dB}$.

第 7 章 振荡器

7-2

1. 第一问

   1. 共基极输出电压同相，变压器同名端反相，故为负反馈，无法产生自激振荡.

   2. 共射极输出电压同相，变压器同名端反相，故为正反馈，有可能产生振荡，属于互感 LC 振荡器.

   3. 发射极相连两个电抗元件同性，但另一个电抗元件也为同性，故无法产生自激振荡.

   4. ce 极接感性元件，因此 be 接感性，bc 接容性. 高频时趋于感性，因此满足

      $${\omega }_2={\displaystyle \frac{1}{\sqrt{L_2{C}_2}}}<{\omega }_{\mathrm{osc}}<{\omega }_1={\displaystyle \frac{1}{\sqrt{L_1{C}_1}}}$$

      时可发生振荡.

   5. 考虑晶体管 be 间的 极间电容，可构成电容三点式振荡器.（但是振荡频率不稳定）

2. 问题二

   1. 不可以，是负反馈.

   2. 不满足一般法则.

   3. 不合理...

备注

• 1.4 是我错了还是答案错了？振荡的时候与发射极相连的都是感性电抗，所以谐振频率应该低于振荡频率吧？

• （2）感觉好怪...

7-3

1. 当 $f_{03}>max\{f_{01},f_{02}\}$$f_{03} > \max\Bqty{f_{01}, f_{02}}$ 时，为电感三点式振荡器，$max\{f_{01},f_{02}\}<f_{\mathrm{osc}}<f_{03}$$\max\Bqty{f_{01}, f_{02}} < f_\rm{osc} < f_{03}$.

2. 当 $f_{03}<min\{f_{01},f_{02}\}$$f_{03} < \min\Bqty{f_{01}, f_{02}}$ 时，为电容三点式振荡器，$f_{03}<f_{\mathrm{osc}}<min\{f_{01},f_{02}\}$$f_{03} < f_\rm{osc} < \min\Bqty{f_{01}, f_{02}}$.

其余情况无法发生振荡.

备注 同 7-2，是我的问题还是答案的问题...

7-5

1. 正反馈，故可能满足振幅条件.

   环路增益的相位为零，故可能满足相位条件.

   LC 并联回路保证了相频特性斜率为负，从而满足相位稳定条件.

   因此电路可以发生振荡.

2. 由矢量图法知，反馈电压与输入电压不同相，因此无法振荡.

3. T₁ 为共基极，T₂ 为共集电极.

   T₁ 未引入反馈，T₂ 引入了负反馈，因此无法振荡.

7-7

7-10

7-13

7-2-1

教材例题，书上有详细解答. ⭐️

第 9 章 调制和解调电路

9-1

不妨认为各线圈匝数比均为 1 : 1.

（a）由

于是无法实现双边带调幅.

（b）由

解得

取双向开关函数基波分量，于是可实现双边带调幅.

包含的频率有：$2k{\omega }_{\mathrm{c}},(2k-1){\omega }_{\mathrm{c}}\pm \mathrm{\Omega },k\in {\mathbb{N}}^{+}$$2k \omega_\rm c, (2k-1) \omega_\rm c \pm \Omega, k \in \N^+$.

（c）可以实现双边带调幅：由

解得

取双向开关函数基波分量，于是可实现双边带调幅.

包含的频率有：$(2k+1){\omega }_{\mathrm{c}}\pm \mathrm{\Omega },{\omega }_{\mathrm{c}},k\in \mathbb{N}$$(2k + 1) \omega_\rm c \pm \Omega, \omega_\rm c, k \in \N$.

（d）由

解得

于是无法实现双边带调幅.

备注 定性分析不需要考虑输出电压的影响. 定量分析则需要考虑（即上述过程）

9-3

若 $v_1(t)$$v_1(t)$ 为大信号，则 D₁ 和 D₂ 管始终无法导通，无法利用二极管桥式电路的特性.

因此 $v_1(t)$$v_1(t)$ 为小信号，大信号 $v_2(t)$$v_2(t)$ 起到开关作用.

（1）作为混频器（以下混频为例）

$v_1(t)=v_{\mathrm{RF}}(t)$$v_1(t) = v_\rm{RF}(t)$ 为射频小信号，$v_2(t)=v_{\mathrm{LO}}(t)$$v_2(t) = v_\rm{LO}(t)$ 为本振大信号.

1. 当二极管未导通时，有

2. 当二极管导通时，由于 $R_{\mathrm{L}}\gg R_{\mathrm{D}}$$R_\rm L \gg R_\rm D$，可认为 $R_{\mathrm{L}}$$R_\rm L$ 一路为开路.