第二次翻转课堂草稿

思考题

（1）如何求解两个信号的卷积？如何确定卷积运算的积分限？

求解卷积: 通过定义, 利用性质, 使用软件.
确定积分限: 使用图解法, 或利用示性函数.

（2）为什么可以利用激励信号和冲激响应的卷积运算求解系统的零状态响应？

见证明.

（3）如何用图解法求解卷积？

见教材.

（4）系统并联和级联时，如何计算总系统的冲激响应？

传输算子
- $H(p) = H_1(p) H_2(p)$ .
- $H(p) = H_1(p) + H_2(p)$ .
单位冲激响应
- $h(t) = h_1(t) * h_2(t)$ .
- $h(t) = h_1(t) + h_2(t)$ .
应用见练习（7）

（5）卷积运算有哪些重要性质？

见笔记.

（6）利用MATLAB模拟例2.16~例子2.18的卷积运算过程（放到U盘中，课上演示）。

2.16 和 2.18 的 MATLAB 代码.

2.17 的 Mathematica 代码.

练习题

以下每一题均提供过程与 mathematica 代码.

（1）C

[f_{1} (t) * f_{2} (t)]^{'} = f_{1}^{'} (t) * f_{2} (t) .


1
D[Convolve[f1[x], f2[x], x, t], t]

（2）D

\begin{aligned} u (t) * u (t) & = \int_{- \infty}^{+ \infty} I_{x \geq 0, t - x \geq 0} d x = \int_{0}^{t} I_{{t \geq x \geq 0}} d x = t u (t), \end{aligned}

$u(t) * u(t-3) = (t-3) u(t - 3)$ , 从而得到 D.


xxxxxxxxxx
1
1
Convolve[UnitStep[x], UnitStep[x] - UnitStep[x - 3], x, t]

（3）B

由（2）中结论,

(f_{1} * f_{2}) (5) = 7 - 6 + 1 - 5 + 2 = - 1.

另外, 不知道为什么, 下面这个代码如果把 t 换成 5, mathematica 就换算不成最简式了.

不过 Simplify 之后还是比较舒服的.


xxxxxxxxxx
5
1
Convolve[
2
    UnitStep[x] - UnitStep[x - 2],
3
    UnitStep[x + 2] - 2 UnitStep[x - 2] + UnitStep[x - 4],
4
    x, t
5
] // Simplify

实际上, 函数的表达式为

\begin{matrix} f_{1} (t) * f_{2} (t) = {\begin{cases} t + 2, & - 2 \leq t < 0, \\ 2, & 0 \leq t < 2, \\ 6 - 2 t, & 2 \leq t < 4, \\ t - 6, & 4 \leq t < 6, \\ 0, & 其 它 . \end{cases} \end{matrix}

（4）A

u (t) * u (t) = \int_{0}^{t} e^{- 4 t} I_{{t \geq x \geq 0}} d x = \frac{1 - e^{- 4 t}}{4} u (t) .


xxxxxxxxxx
1
1
Convolve[E^(-4 x) UnitStep[x], UnitStep[x], x, t]

（5）

\begin{aligned} f (t) * δ_{T} (t) & = \sum_{m = - \infty}^{+ \infty} f (t - m T) . \end{aligned}

$0 < T < {\tau}$ 时, 有重叠, 可按重叠次数进一步划分.
$T = \tau$ 时, 恰好无重叠.
$T > \tau$ 时, 每个三角波之间都有间距.

$\tau = 2$ $m$ 的系数即可绘出不同情况的波形图.


xxxxxxxxxx
1
1
Plot[Sum[HeavisideLambda[t - 2 m], {m, -10, 10, 1}], {t, -3, 3}]

（6）由（2）中结论,

\begin{aligned} f (t) & = u (t) - 2 u (t - 1) + u (t - 2), \\ h (t) & = u (t) - u (t - 1), \\ g (t) & = - (t - 3) u (t - 3) + (t - 2) u (t - 2) - (t - 1) u (t - 1) - \\ 2 (t - 1) u (t - 1) + 2 (t - 2) u (t - 2) + t u (t) \\ = - (t - 3) u (t - 3) + 3 (t - 2) u (t - 2) - 3 (t - 1) u (t - 1) + t u (t) \\ = {\begin{cases} t, & 0 \leq t < 1, \\ 3 - 2 t, & 1 \leq t < 2, \\ t - 3, & 2 \leq t < 3, \\ 0, & 其 它 . \end{cases} \end{aligned}


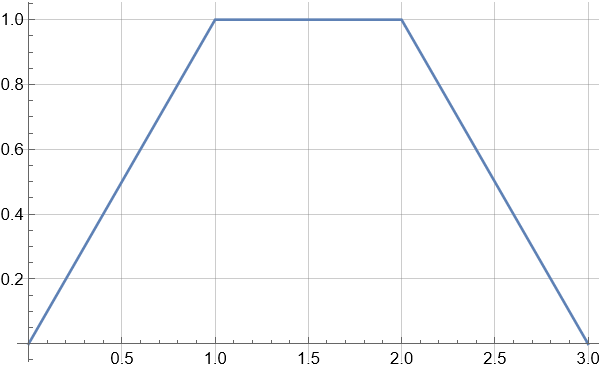
xxxxxxxxxx
5
1
Convolve[
2
    UnitStep[x] - 2 UnitStep[x - 1] + UnitStep[x - 2],
3
    UnitStep[x] - UnitStep[x - 1],
4
    x, t
5
] // Simplify

（7）

\begin{aligned} h_{1} (t) & = u (t) - u (t - 1), \\ h_{2} (t) & = u (t - 1) - u (t - 2), \\ h (t) & = h_{1} (t) * h_{1} (t) + h_{1} (t) * h_{2} (t) \\ = [u (t) - u (t - 1)] * [u (t) - u (t - 2)] \\ = t u (t) - (t - 1) u (t - 1) - (t - 2) u (t - 2) + (t - 3) u (t - 3) \\ = {\begin{cases} t, & 0 \leq t < 1, \\ 1, & 1 \leq t < 2, \\ 3 - t, & 2 \leq t < 3, \\ 0, & 其 它 . \end{cases} \end{aligned}


xxxxxxxxxx
9
1
f = Convolve[
2
    UnitStep[x] - UnitStep[x - 1],
3
    UnitStep[x] - UnitStep[x - 2],
4
    x, t
5
] // Simplify
6
Plot[
7
    f, {t, 0, 3},
8
    GridLines -> {Automatic, Automatic}
9
] (* 不知道为什么, Convolve 直接写到 Plot 里面就画不出来图像 *)