复分析
第 1 章 复数1.1 复数代数1.2 复数的几何表示第 2 章 复函数2.1 解析函数2.1.1 解析函数的充要条件2.1.2 复变函数的性质2.1.3 多项式2.1.4 有理函数2.2 幂级数2.3 指数函数与三角函数2.3.1 指数函数2.3.2 三角函数2.3.3 双曲三角2.3.4 对数函数第 3 章 作为映射的解析函数3.1 初等点集拓扑3.1.1 度量空间3.1.2 点集
第 1 章 复数
1.1 复数代数
虚数单位
故凡是以复数为中间推导的算法 (如离散傅里叶变换), 将
注: 以下均以希腊字母表示实数, 以英文字母表示复数, 不加说明时默认
运算
加法 / 减法
乘法
除法
平方根
定义
共轭
对于任意有理函数
实部 / 虚部
模
拉格朗日恒等式
不等式
三角不等式
当且仅当
推论
柯西不等式
证法一: 由拉格朗日恒等式即得.
证法二: 由
证法三: 由数学归纳法即得.
1.2 复数的几何表示
平几表示
概念
坐标
幅角
极坐标
运算
几何加法: 向量相加.
几何乘法: 幅角相加模相乘.
注意: 如果用点表示复数, 则
应用
二项方程
棣莫弗公式
开根
解析几何
圆
直线
两直线夹角:
平行线距离:
点到线的距离: 同平行线间距离公式.
椭圆
双曲线
抛物线
球面表示
无穷远点: 没有一个半平面包含这个理想点.
黎曼球面
球极平面投影:
球面上任一圆, 对应平面上一个圆或一条直线.
若球上一圆所在平面为
复数在球极平面投影的距离
注: 可由相似得第二式, 再由两次余弦定理得第一式, 后者无需借助球极射影, 计算量很小.
其它性质
第 2 章 复函数
2.1 解析函数
2.1.1 解析函数的充要条件
若函数记为
柯西黎曼微分方程组
因此可将导数及其模表示为
解析函数的导数也是解析的,
因此解析函数的实部与虚部满足拉普拉斯方程, 称为 共轭调和函数.
函数
2.1.2 复变函数的性质
复变量的实函数的导数要么为零, 要么不存在.
不为常数的解析函数的模不可能为常数.
若
和差:
乘积:
商式:
复合:
求导:
调和与解析
若
若
若
实部与虚部
已知实部
法一: 利用柯西黎曼微分方程组两次积分.
法二: 利用
若
2.1.3 多项式
多项式是解析函数.
知识回顾
代数学基本定理
引理: 如果
推论:
如果
卢卡斯定理 如果多项式
推论: 包含
2.1.4 有理函数
分母的零点称为有理函数极点, 扩充平面中的极点个数称为有理函数的阶数.
线性变换
一阶有理函数:
平行移动:
逆:
部分分式展开法
将有理分式表示为
求出所有极点, 记为
类似的, 有
于是
第一节习题
在圆
在圆
2.2 幂级数
序列
基本序列 (柯西序列:
序列收敛当且仅当其为柯西序列.
序列的收缩
常数项级数
绝对收敛级数的和, 在重排后不变.
函数项级数
点态收敛
一致收敛
一致收敛的连续函数序列, 其极限函数也连续.
一致收敛
魏尔斯特拉斯 M 判别法
若
若强级数收敛, 则弱级数一致收敛.
幂级数
阿贝尔第一定理: 对于每个幂级数,
当
当
当
当
阿达马公式:
麦克劳林展开式
阿贝尔第二定理: 如果
不太懂.
第二节习题
若
若
若
2.3 指数函数与三角函数
2.3.1 指数函数
定义:
习惯上, 也可以用
级数展开:
证明: 归纳法得系数, 阿贝尔定理证收敛.
加法定理:
证明:
取值范围:
证明:
共轭:
证明: 由级数展开即得.
取模:
证明:
最小正周期:
2.3.2 三角函数
定义:
级数展开
上二式每一个余项有与首项相同的符号.
欧拉公式:
备注:
上述所有公式都是耳熟能详的, 这里的重点是推广到复数的构造方式. 其余若干结论不再赘述, 可以参考我的三角学笔记 (暂时未上传, 所以没有超链接).
采取这样的定义, 可以避免许多级数敛散性与一致收敛性的讨论, 并且复平面上正余弦的加法公式可以作为欧拉公式的直接推论, 而不构成循环论证.
但要注意, 实数上正余弦的加法公式并非其推论, 因为我们首先要证明上述复数域中定义的正余弦在实数上的取值与实数域上定义的正余弦相同, 而这一步需要正弦的导数, 但在计算导数时用到了加法公式, 从而构成循环论证.
类似的, 不能用洛必达法则求第一个重要极限公式, 因为正弦导数的推导中同样用到了这一极限.
欧拉公式可以被证明, 前提是有合适的定义. 这里通过微分方程定义复变指数函数, 也可以通过欧拉公式或级数去定义, 三者是等价的.
抛开定义谈定理, 都是耍流氓.
2.3.3 双曲三角
定义:
"欧拉公式":
与三角函数的关系
其它结论以后再整理, 下亿次一定.
2.3.4 对数函数
定义:
备注:
一般认为首字母小写为单值, 大写为多值, 如幅角
本质上只有一个初等超越函数.
第 3 章 作为映射的解析函数
3.1 初等点集拓扑
3.1.1 度量空间
定义
例子
黎曼球面上球极象的欧氏距离.
定义在区间
性质
如果
在同一个空间
若
3.1.2 点集
球:
邻域: 集
开集: 一个集合如果是其每个元素的邻域, 则称为开集.
每一个球是一个开集, 称为开球.
空集时开集, 单点集是闭集.
它们都是连通集.
补集:
闭集: 开集之补.
有限多个开集之交是开的.
任意多个开集之并是开的.
有限多个闭集之并是闭的.
任意多个闭集之交是闭的.
内部: 最大子开集, 或所有子开集之并, 记为
闭包: 最小父闭集, 或所有父闭集之交, 记为
边界:
外部:
孤立点: 若
聚点: 闭集与孤立点的差集.
任意集合的聚点构成闭集.
离散集: 所有点都是孤立点的集合.
欧氏空间的任一离散子集可数.
证明:
可数集合不一定离散.
如
例子
离散集
3.1.3 连通性
子空间的概念: 相对邻域, 相对开集, 相对拓扑.
连通: 不能表示成无交非空相对开集之并的度量空间子集称为是连通的.
性质
开集连通
闭集连通
例子: 空集, 单点集,
定理
实线的非空连通子集是区间.
实数的任一非空有界闭集必有一个极小值与一个极大值.
平面上的一个非空开集连通, 当且仅当该集中的任意两点可用整个位于该集内的折线连接起来.
下界: 若
设所有下界组成集
当
当
当
类似的有上界与上确界
域: 非空连通开集称为域 (region).
与代数系统中的域 (field) 不同.
闭域: 即域的闭包.
不同的域可以有相同的闭包.
分集: 不包含在任何更大的连通子集中的连通子集.
不同的分集无交.
定理
每一个集具有唯一的分成分集的分解.
局部连通空间的子开集的分集是开的.
局部连通: 若集中任一点
局部连通可分空间中, 每个开集是不相交区域的可数并.
3.1.4 紧致性
敛散性
如果
如果
收敛序列是柯西序列.
完备性
完备性: 所有柯西序列收敛的度量空间称为是完备的.
度量空间的完备子集是闭的,
完备空间的闭子集是完备的.
紧致性
开覆盖: 如果集合
紧致性: 每一个开覆盖包含一个有穷子覆盖的集合称为是紧致的, 又称为 海涅 - 博雷尔性质.
全有界性: 对于任一
全有界集必是有界集.
全有界集任一子集全有界.
紧致
极限点: 称
波尔查诺 - 魏尔斯特拉斯定理: 一个度量空间是紧致的, 当且仅当每个无穷序列具有一个极限点.
紧致的第三种定义.复数的每个有界序列具有一个收敛的子序列.
3.1.5 连续函数
函数 (映射)
令
注意
注意
若定义域为扩充复平面, 则通常的距离应换为黎曼球面的距离.
连续:
一个函数是连续的, 当且仅当每一个开集的逆象是开的.
一个函数是连续的, 当且仅当每一个闭集的逆象是闭的.
一致连续:
定理
连续映射下, 任一紧致集的象必是紧致的, 因而是闭的.
紧致集上一个实值连续函数必有一个极大值和一个极小值.
在连续映射下, 任一连通集的象是连通的.
在连通集上连续的非零实值函数或者恒正或者恒负.
紧致集上的连续函数一致连续.
拓扑映射 (同胚映射)
如果映射
拓扑性质: 为这个集所有拓扑映像所共有的性质.
拓扑性质: 紧致性, 连通性.
非拓扑性质: 是开子集.
当
3.1.6 拓扑空间
拓扑空间: 一个集
空集
任何两个开集之交是一个开集.
任意多个开集之并是一个开集.
相关定义:
闭集是开集的余集.
邻域: 如果存在一个开集
连通性由开集定义, 故相关定理仍保持正确, 如海涅 - 博雷尔性质.
豪斯多夫空间: 任意两个相异的点包含在无交开集之中的拓扑空间.
在豪斯多夫空间中, 收敛序列的极限唯一.
3.2 共形性
3.2.1 弧与闭曲线
平面中弧的表示
参数变换
变换可逆, 当且仅当
弧的起点和终点经参数变换后保持不变.
导数
可微: 导数存在且连续的弧称是可微的.
正则:
分段可微与分段正则: 对除去有穷个
导数极限定理: 若导数的单侧极限存在, 则其等于函数的单侧导数.
若
特殊的弧
简单弧 (若尔当弧):
闭曲线: 弧的两端点重合.
闭曲线的移换:
反向弧
点曲线: 常值函数
有限圆:
3.2.2 域内的解析函数
定义
点集拓扑: 定义在开集
扩充平面: 在区域
扩充平面: 在复数开子集上导数极限处处存在的函数称为 全纯函数.
全纯函数与亚纯函数也称为 (复) 解析函数.
可在合适的域中定义多值函数的单值分支, 进而证明连续与解析.
退化: 在域
如果域内解析函数满足以下任一条件, 则函数必是一常数: 🌙
导数恒等于零.
实部或虚部为零.
模或幅角为零.
如果
3.2.3 共形映射
求导
夹角
因此, 在
比例
在一点的比例与方向无关.
求偏导
保持角度不改变:
比例与方向无关:
右式取正号时,
间接共形保持大小不变, 角度符号相反.
拓扑
如果解析函数
如果映射限制在
如果映射限制在整个区域
3.2.4 长度和面积
长度
曲线
象曲线
面积
面积
象面积
3.3 线性变换
3.3.1 线性群
分式线性变换 (莫比乌斯变换)
不考虑零变换 (奇异变换).
可作为约定而引入, 也可作为极限而引入.
线性变换的矩阵表示
通过齐次坐标
线性变换组成一般线性群
如果
线性变换群是复数的一维射影群, 记为
复数的线性变换中,
特殊的线性变换
平行移动
旋转缩放
当
当
反演变换
线性变换由平移、复反演、旋转缩放、平移组成.
不是线性变换的例子
反射
几何反演
3.3.2 交比
交比: 在互异的三点
定理
将
也可以利用
交比
圆和直线在黎曼直线上都对应于圆, 可统称为圆.
线性变换将圆变为圆.
性质: 记
且
推论 1:
推论 2: 托勒密定理
推论 3: 托勒密不等式
推论 4: 任意四个相异点可用六种方式线性变换至
3.3.3 对称性
对称性: 点
解释
即线性变换圆
补充
把点
两个反射组成一个线性变换.
对称性的几何意义
线:
证明
圆:
证明
对称原理: 如果一个线性变换将一个圆
应用 1: 已知对称, 求象.
已知
已知
注意对称轴有无数条.
应用 2: 给定两圆, 求变换.
已知圆上三点, 则变换为
已知圆上一点和不在圆心和圆上的一点, 则变换为
例题
将圆
3.3.4 有向圆
保角性: 由于线性变换
定向
根据圆
根据
左边的点组成圆的内部.
右边的点组成圆的外部.
性质
若画出箭头, 由
若
3.3.5 圆族
圆网 (施泰纳圆族) 的组成
圆族
将线性变换表示为
圆族
同心圆
这些圆称为阿波罗尼奥斯圆, 记为
备注
上述线性变换只作引入概念用, 下文的
施泰纳圆族的性质
通过平面上除了极限点以外的每个点, 只有一个
每一个
在关于一个
在关于一个
极限点关于每一个
施泰纳圆族的变换
不动点
如果一线性变换
当
相反, 可以通过求解
上式中
变换
当
当
具有两个不动点的一般线性变换是具有相同不动点的双曲变换和椭圆变换的乘积.
当
考虑变换
直线族
两直线族的直线彼此正交, 因此
直线
将
若
不是双曲的、椭圆的、抛物型的线性变换称为斜驶变换.
3.4 初等共形映射
3.4.1 阶层曲线
对于解析函数
幂函数
将围绕原点的同心圆变为同族的圆.
将原点引出的半直线变为同族的半直线,
二次幂:
阶层曲线
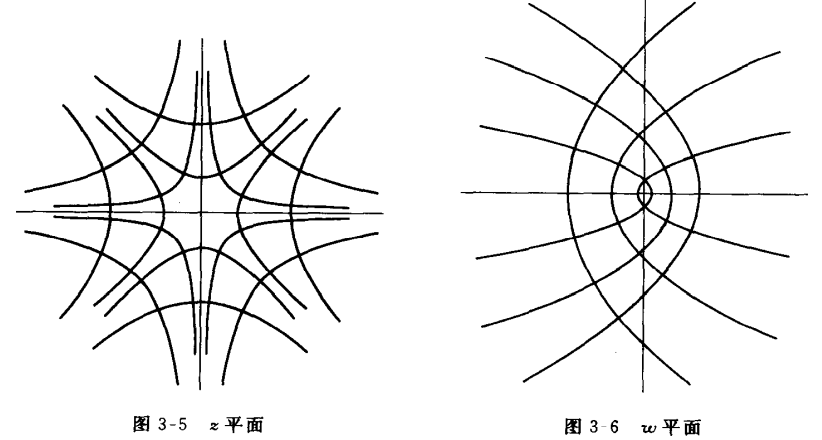
其正交族为
三次幂
如下作图为
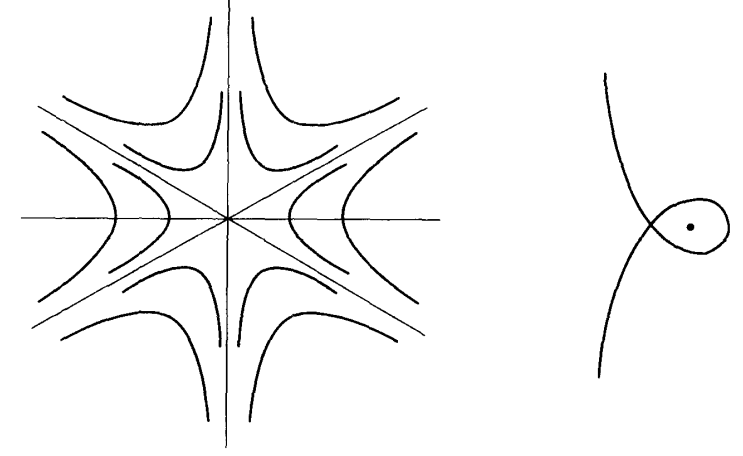
指数函数
直线的象
其它直线被映为对数螺线.
域的象
将带映为单位圆盘
3.4.2 初等映射
共形映射的一般问题可以化为将一个域映成圆盘或半平面的问题.
圆楔形: 以两条共端点的圆弧为边界的域
莫比乌斯变换
幂变换
切于
莫比乌斯变换
指数变换将平行带映为半平面.
一个线段的补区域, 即角为
映射的步骤
设其端点为
定义平方根
综上,
令
由上式分别消去
三次多项式的映射
3.4.3 初等黎曼面
叶又称为层.
基本域: 在一一对应下映成具有一个或几个割痕的整个平面的域.
第 4 章 复积分
4.1 基本定理
4.1.1 线积分
1 实区间的积分
设
证明
第二式由定义展开即得, 第三式考虑
令
2 第二型线积分
设分段可微弧
3 二重共轭符号
4 第一型线积分
弧长
对于圆
4.1.2 可求长的弧
弧长还可定义为
如果上确界有穷, 则称该弧是可求长的.
若
弧
4.1.3 线积分作为弧的函数
对于
线积分只依赖于端点.
沿任一闭曲线积分值为零.
恰当微分 (全微分):
例子 ⭐️
对于所有的闭曲线
当
对于圆
计算单位圆上的积分时, 可以利用
若
4.1.4 矩形的柯西定理
矩形
定理 2 (柯西定理) 若
定理 3 从矩形
则
4.1.5 圆盘的柯西定理
记开圆盘
定理 4 设
定理 5 设
则
4.2 柯西积分公式
4.2.1 一点关于闭曲线的指数
引理 1 如果一条分段可微的闭曲线
定义 (指数) 点
卷绕数的性质
若
将
引理 2 设
4.2.2 积分公式
定理 6 ⭐️ 设
推论 (表示公式) 当
柯西积分公式 将上式改写为
备注 在可视化复分析第二章中, 我们学过高斯平均值定理:
高斯平均值定理
幂级数的和式在收敛开圆盘内解析, 同时解析函数可展开为收敛幂级数, 因此高斯平均值定理与柯西积分公式等价.
同样的, 高斯平均值定理计算的上述积分也可以由柯西积分公式得到, 如
4.2.3 高阶导数
引理 3 设
在
推论 由表示公式即得
莫雷拉定理 设
柯西估值 设圆
刘维尔定理 在整个平面中有界的解析函数必是一个常数.
备注 由刘维尔定理可以引出代数基本定理: 设
定理 设函数
关于
4.3 解析函数的局部性质
4.3.1 可去奇点与泰勒定理
定理 7 设
记
定理 8 设
其中
4.3.2 零点和极点
定义 (零点) 若
不恒等于零的解析函数不存在无穷阶零点, 并且各个零点都是孤立的.
唯一性定理 设
换言之, 一个解析函数可以用它在任何一个集上的值唯一确定, 只要这个集有一个聚点包含在解析域中.
定义 (正则) 如果点
定义 (极点) 如果
定义 (亚纯函数) 一个在域
在
两个亚纯函数的和差积商都是亚纯的.