概统笔记附录

附录A.1 常用积分A.2 常用分布A.2.1 一维离散型1 二项分布2 泊松分布3 超几何分布4 负二项分布5 几何分布5' 几何分布6 泽塔分布A.2.2 一维连续型1 正态分布2 指数分布3 混合指数分布4 均匀分布5 对数正态分布6 柯西分布7 拉普拉斯分布8 卡方分布9 t 分布10 F 分布11 贝塔分布12 伽马分布13 威布尔分布14 瑞利分布15 帕累托分布16 逻辑斯蒂分布17 广义贝塔分布其它分布A.2.3 多维离散型1 多项分布A.2.4 多维连续型1 矩形均匀分布2 二维正态分布3 多元正态分布4 狄利克雷分布A.3 常用分布统计表A.3.1 标准正态分布表A.3.2 卡方分布表A.3.3 t 分布表A.3.4 F 分布表1 上 0.1 分位数2 上 0.05 分位数3 上 0.025 分位数4 上 0.01 分位数5 上 0.005 分位数A.4 数列和常数A.4.1 数列卡特兰数A.4.2 常数卡特兰常数

附录

A.1 常用积分

特殊函数的性质 伽马函数与贝塔函数.

\begin{array}{lll} 伽马函数与递推式: & Γ (x) = \int_{0}^{+ \infty} e^{- t} t^{x - 1} d t = (x - 1) Γ (x - 1) & (x > 0) \\ 贝塔函数与关系式: & B (x, y) = \int_{0}^{1} t^{x - 1} (1 - t)^{y - 1} d t = \frac{Γ (x) Γ (y)}{Γ (x + y)} & (x, y > 0) \\ 勒让德倍量公式: & Γ (s) Γ (s + \frac{1}{2}) = \frac{\sqrt{π}}{2^{2 n - 1}} Γ (2 s) & (s > 0) \\ 余元公式: & B (s, 1 - s) = Γ (s) Γ (1 - s) = \frac{π}{\sin π s} & (0 < s < 1) \end{array}

{\begin{cases} Γ (n) = (n - 1)!, & n \in N^{+}, \\ Γ (\frac{n}{2}) = \frac{(n - 2)!!}{2^{(n - 1) / 2}} \sqrt{π}, & n 为正奇数. \end{cases}

B (s, s) = \frac{1}{2^{2 n - 1}} B (\frac{1}{2}, s) (s > 0)

更多内容可以参考 Euler 积分笔记.

特殊函数的应用

一般的

\begin{aligned} \int_{0}^{1} x^{a} (1 - x^{b})^{c} d x = \frac{1}{b} B (\frac{a + 1}{b}, c + 1) & (a > - 1, b > 0, c > - 1) \\ \int_{0}^{+ \infty} \frac{x^{a} d x}{(1 + x^{b})^{c}} = \frac{1}{| b |} B (c - \frac{a + 1}{b}, \frac{a + 1}{b}) & (\begin{array}{c} a > - 1, b > 0, c > \frac{a + 1}{b} & 或 \\ a < - 1, b < 0, c > \frac{a + 1}{b} \end{array}) \\ \int_{0}^{+ \infty} x^{n} e^{- a x^{p}} d x = \frac{Γ (\frac{n + 1}{p})}{| p | a^{\frac{n + 1}{p}}} & (\begin{array}{c} a > 0, p > 0, n > - 1 & 或 \\ a > 0, p < 0, n < - 1 \end{array}) \end{aligned}

特殊的

\begin{aligned} \int_{- \infty}^{+ \infty} \frac{x^{m} d x}{(1 + x^{2})^{n}} = B (n - \frac{m + 1}{2}, \frac{m + 1}{2}) & (注意积分限) \\ \int_{0}^{+ \infty} \frac{x^{m} d x}{(1 + x)^{n}} = B (n - m - 1, m + 1) \end{aligned}

\begin{aligned} \int_{0}^{+ \infty} e^{- a x^{p}} d x = \frac{Γ (\frac{1}{p})}{p a^{\frac{1}{p}}} \\ \int_{0}^{+ \infty} e^{- x^{p}} d x = \frac{1}{p} Γ (\frac{1}{p}) \\ \int_{- \infty}^{+ \infty} e^{- a x^{2}} d x = \sqrt{\frac{π}{a}} (注意积分限) \end{aligned}

\begin{aligned} \int_{0}^{+ \infty} x^{n} e^{- a x} = \frac{Γ (n + 1)}{a^{n + 1}} = \frac{n!}{a^{n + 1}} \\ \int_{0}^{+ \infty} x^{n} e^{- a x^{2}} = \frac{Γ (\frac{n + 1}{2})}{2 a^{\frac{n + 1}{2}}} \\ \int_{0}^{+ \infty} x^{2 n} e^{- a x^{2}} d x = \frac{(2 n - 1)!!}{2 (2 a)^{n}} \sqrt{\frac{π}{a}} \\ \int_{0}^{+ \infty} x^{2 n + 1} e^{- a x^{2}} d x = \frac{(2 n)!!}{(2 a)^{n + 1}} \\ \int_{0}^{+ \infty} x^{2} e^{- a x^{2}} d x = \frac{1}{4 a} \sqrt{\frac{π}{a}} \end{aligned}

有关 Catalan 常数的积分.

A.2 常用分布

定义说明

$\mu := E(X)$ .
$\sigma^2 := E[(X - \mu)^2]$ .
$k$ $\alpha_k := E(X^k)$ .
$k$ $\mu_k := E[(X-\mu)^k]$ .
$\beta_1 = \dfrac{\mu_3}{\sigma^3}$ .
$\beta_2 := \dfrac{\mu_4}{\sigma^4} = \dfrac{\mu_4}{\mu_2^2}$ .
$v_c := \dfrac{\sigma}{\mu}$ .

A.2.1 一维离散型

1 二项分布

1.1 基础概念

$X \sim B(n, p)$ .
$p$ $n$ $x$ .
$\displaystyle P(X=i) = b(i; n, p) = \binom{n}{i} p^i (1-p)^{n-i}$ .

1.2 数字特征

$x = \left\lfloor (n+1)p \right\rfloor$ .
$E(X) = np$ .
$\Var(X) = np(1-p)$ .
$G(s) = (ps + q)^n, q = 1 - p %s \in (-\infty, +\infty)$ .
$g(t) = (p\e^{\i t} + q)^n$ .

1.3 其它性质

二项分布和的函数
$X_1 \sim B(n_1, p),\, X_2 \sim B(n_2, p) \QRA X_1 + X_2 \sim B(n_1+n_2, p)$ .
$p_n = \dfrac{1}{2}[1+(1-2p)^n]$ .
$f(p) = P(X \le k)$ $f'(p) < 0$ , 并且
$f (p) = \frac{n!}{k! (n - k - 1)!} \int_{0}^{1 - p} t^{k} (1 - t)^{n - k - 1} d t .$

1.4 参数估计

$p = m/n$ . (MVU 估计)
$p = m/n$ . (MVU 估计)
贝叶斯估计
- $p = \dfrac{X+1}{n+2}$ .
- $h(p) = p^{a-1}(1-p)^{b-a-1}$ $\tilde{p} = \dfrac{X+c}{n+d}$ .
区间估计
- $\dfrac{X - np}{\sqrt{np(1-p)}} \sim N(0, 1)$ , 解不等式得
  $(1 + \frac{z_{α / 2}^{2}}{n}) p^{2} - (2 X + \frac{z_{α / 2}^{2}}{n}) p + X^{2} < 0$ $\begin{aligned} {\hat{p}}_{1}, {\hat{p}}_{2} & = \frac{n}{n + z_{α / 2}^{2}} (\overset{―}{X} + \frac{z_{α / 2}^{2}}{2 n} \pm z_{α / 2} \sqrt{\frac{\overset{―}{X} (1 - \overset{―}{X})}{n} + \frac{z_{α / 2}^{2}}{4 n^{2}}}) \\ \approx \overset{―}{X} \pm z_{α / 2} \sqrt{\frac{\overset{―}{X} (1 - \overset{―}{X})}{n}} . \end{aligned}$
$p^k\; (k \le n)$ $\dfrac{X^\underline{k}}{n^{\underline{k}}}$ . (下降阶乘幂)

2 泊松分布

2.1 基础概念

$X \sim P(\lambda)$ .
$\lambda$ $x$ .
$\displaystyle P(X=i) = \lim_{n\to\infty} b(i; n, \frac{\lambda}{n}) = \dfrac{\e^{-\lambda}\lambda^i}{i!}$ .
$n>50, p<0.1, np<5$ 时, 用泊松分布近似效果较好.

2.2 数字特征

$k = \floor{\lambda}$ .
$E(X) = \lambda$ .
$\Var(X) = \lambda$ .
$m_e = \dfrac{\ln 2\lambda}{\lambda}$ .
$E\vqty{X - m_e} = m_e$ .
$G(s) = \e^{\lambda(s-1)},\, s \in (-\infty, +\infty)$ .
$g(t) = \e^{\lambda\pqty{\e^{\i t} - 1}}$ .

2.3 其它性质

泊松分布和的函数 (可加性)
$X_1 \sim P(\lambda_1),\, X_2 \sim P(\lambda_2) \QRA X_1 + X_2 \sim P(\lambda_1 + \lambda_2)$ .
$f(\lambda) = P(X \le k)$ $f'(\lambda) < 0$ $f(\lambda) = \dfrac{1}{k!} \dint_\lambda^{+\infty} t^k \e^{-t} \dt$ .
注: 上式可用于参数检验.
$P_\lambda(X \le k) = \dsum_{i=0}^{k} \dfrac{\e^{-\lambda} \lambda^i}{i!} = \dint_\lambda^{+\infty} \dfrac{\e^{-t}t^k}{k^!} \dt = K_{2k + 2}(2\lambda)$ . (卡方分布函数)
$X \sim P(\lambda),\, Y \sim B(X, p)$ $Y \sim P(\lambda p)$ .
$T>0$ $T$ $X \sim P(\lambda T)$ $P(X = n) = \dfrac{\e^{-\lambda T} (\lambda T)^n}{n!}$ $%用归纳法.$
泊松分布的一个应用见特殊函数笔记中的 Dobinski 公式.

2.4 参数估计

矩估计
- $\lambda = m$ . (MVU 估计)
- $\lambda = m_2$ $S^2$ .
$\lambda = \overline{X}$ .
贝叶斯估计: 见第四章第五题.
区间估计
- $(Y_n - n\lambda) / \sqrt{n\lambda} \sim N(0, 1)$ , 则
  $A, B = \overset{―}{X} + u_{α / 2}^{2} / (2 n) \pm u_{α / 2} \sqrt{u_{α / 2}^{2} / (4 n^{2}) + \overset{―}{X} / n}, \overset{―}{X} = Y_{n} / n .$

3 超几何分布

3.1 基础概念

$X \sim H(N, n, M)$ .
$N$ $M$ $n$ $m$ .
$\displaystyle P(X=m) = \binom{M}{m} \binom{N-M}{n-m} \left/ \binom{N}{n} \right.$ .

3.2 数字特征

$E(X) = \dfrac{nM}{N}$ .
$\Var(X) = \dfrac{nM(N-n)(N-M)}{N^2(N-1)} = \dfrac{nM}{N} \dfrac{N-n}{N-1} \pqty{1- \dfrac{M}{N}}$ .

3.3 其它性质

3.4 参数估计

$N,\, n$ $M$ .

$M = \dfrac{N+2}{n+2}(X+1) - 1$ .

4 负二项分布

4.1 基础概念

$X \sim NB(r, p)$ , 又称为正整数形式帕斯卡分布.
$p$ $r$ 不合格产品 $x$ .
$\displaystyle P(X=i) = d(i; r, p) = \binom{i+r-1}{r-1}p^r(1-p)^i$ .

4.2 数字特征

$E(X) = \dfrac{r(1-p)}{p}$ .
$\Var(X) = \dfrac{r(1-p)}{p^2}$ .

4.3 其它性质

4.4 参数估计

$m_e := (\splus{X}{n})/n$ .

$p = \dfrac{r}{m_e+r}$ .
$p = \dfrac{r}{m_e+r}$ .
$p = \dfrac{nr+1}{nr+nm_e+1}$ .

5 几何分布

5.1 基础概念

$X \sim GE(p)$ .
$p$ 不合格产品 $x$ .
$P(X=i) = p(1-p)^{i}$ .
$P(X \le k) = 1 - (1-p)^{k+1}$ .
$P(X \ge k) = (1 - p)^k$ .

5.2 数字特征

$E(X) = \dfrac{1-p}{p}$ .
$\Var(X) = \dfrac{1-p}{p^2}$ .
$G(s) = \dfrac{ps}{1-qs} - 1,\, s \in \pqty{-\dfrac{1}{q}, \dfrac{1}{q}}$ .
$g(t) = \dfrac{p\e^{\i t}}{1 - q\e^{\i t}} - 1$ .

5.3 其它性质

几何分布具有无记忆性.
$\soneto{X}{r}$ $GE(p)$ $\splus{X}{r} \sim NB(r, p)$ .
$X_1 \sim \mathrm{GE}(1 - p_1)$ $X_2 \sim \mathrm{GE}(1 - p_2)$ 独立, 则
$\begin{aligned} min (X_{1}, X_{2}) \sim GE (1 - p_{1} p_{2}) \\ max (X_{1}, X_{2}) \sim P (X = k) = p_{1}^{k} (1 - p_{1}) + p_{2}^{k} (1 - p_{2}) + p_{1}^{k} p_{2}^{k} (p_{1} p_{2} - 1) \end{aligned}$
$X_i \sim \mathrm{GE}(1 - p_i)$ $\min_i(X_i) = \mathrm{GE}(1 - \prod_i p_i)$ .

5' 几何分布

5'.1 基础概念

$X \sim G(p)$ .
$p$ 总产品 $x$ .
$P(X=i) = p(1-p)^{i-1}$ .

5'.2 数字特征

$E(X) = \dfrac{1}{p}$ .
$\Var(X) = \dfrac{1-p}{p^2}$ .
母函数
- $G(s) = \dfrac{ps}{1-qs},\, s \in \pqty{-\dfrac{1}{q}, \dfrac{1}{q}}$ .
- $G^{(n)}(1) = \dfrac{(1-p)^{n-1}}{p^n} n!$ .
$g(t) = \dfrac{p\e^{\i t}}{1 - q\e^{\i t}}$ .

5'.3 其它性质

几何分布具有无记忆性.
$\soneto{X}{r}$ $G(p)$ $\splus{X}{r} - r \sim NB(r, p)$ .

6 泽塔分布

6.1 基础概念

$X \sim \mathrm{Zeta}(s)$ .
$\zeta(s) = \nsum \dfrac{1}{n^s}$ .
$P(X = k) = \dfrac{1}{\zeta(s) k^s},\, k = 1, 2, \cdots$ .

6.2 数字特征

$k$ $E(X^k) = \dfrac{\zeta(s-k)}{\zeta(s)},\, s > k + 1$ .
$E(\ln{X}) = -\dfrac{\zeta'(s)}{\zeta(s)},\, s > 1$ .
$H(X) = E(-\ln(\mathrm{Zeta}(s))) = -\dsum_{k=1}^\infty \dfrac{\ln \frac{1}{\zeta(s) k^s}}{\zeta(s) k^s} = \ln\zeta(s) - s\dfrac{\zeta'(s)}{\zeta(s)}$ .

6.3 其它性质

问题 1 (最大熵分布)
对于取值为正整数的概率分布, 求给定对数期望的条件下熵最大的分布, 即
$\begin{matrix} max = - \sum_{k} p_{k} \ln p_{k} \\ {\begin{cases} \sum_{k} p_{k} = 1, \\ \sum_{k} p_{k} \ln k = a . \end{cases} \end{matrix}$
由 Lagrange 乘数法解得此分布即为 Zeta 分布.
性质 1
$X \sim \mathrm{Zeta}(s)$ $p$ 的指数满足:
$ν_{p} (X) \sim GE (1 - p^{- s}) .$
证明
$\begin{aligned} P (ν_{p} (X) \geq k) & = \frac{1}{ζ (s)} \sum_{n = 1}^{\infty} \frac{1}{(p^{k} n)^{s}} = \frac{1}{p^{k s}} \\ P (ν_{p} (X) = k) & = \frac{1}{p^{k s}} - \frac{1}{p^{(k + 1) s}} = (1 - p^{- s}) p^{- k s} \end{aligned}$
性质 2
$X \sim \mathrm{Zeta}(s)$ $p$ $q$ $\nu_p(X)$ $\nu_q(X)$ 独立.
证明
$P (ν_{p} (X) \geq k, ν_{q} (X) \geq l) = \frac{1}{(p^{k} q^{l})^{s}} = \frac{1}{p^{k s} p^{l s}} = P (ν_{p} (X) \geq k) P (ν_{q} (X) \geq l) .$
性质 3
$\mathbb{P}$ $\Bqty{X_p}_{p \in \mathbb{P}}$ $X_p \sim \mathrm{GE}(1 - p^{-s})$ , 则
$Z = \prod_{p \in P} p^{X (1 - p^{- s})} \sim Z (s) .$
证明 $\dfrac{1}{\zeta(s)} = \dprod_{p \in \mathbb{P}} \pqty{1 - \dfrac{1}{p^s}}$ 得:
$P (Z = k) = \prod_{p \in P} (1 - \frac{1}{p^{s}}) \frac{1}{p^{ν_{p} (k) s}} = \frac{1}{ζ (s)} \prod_{p \in P} \frac{1}{p^{ν_{p} (x) s}} = \frac{1}{ζ (s) k^{s}} .$
性质 4
$X_1 \sim \mathrm{Zeta}(s_1)$ $X_2 \sim \mathrm{Zeta}(s_2)$ 独立, 则
$gcd (X_{1}, X_{2}) \sim Zeta (s_{1} + s_{2}) .$
证明
$ν_{p} (gcd (X_{1}, X_{2})) = min {ν_{p} (X_{1}), ν_{p} (X_{2})} \sim GE (1 - p^{- (s_{1} + s_{2})}) .$
问题 2 (两个随机的正整数互素的概率)
$X$ $Y$ $\QRLA \gcd(X, Y) = 1$ .
$\sim \lim\limits_{s \to 1^+} \mathrm{Zeta}(s)$ .
$lim_{s_{1}, s_{2} \to 1^{+}} P (gcd (X, Y) = 1) = lim_{s_{1}, s_{2} \to 1^{+}} \frac{1}{ζ (s_{1} + s_{2})} = \frac{1}{ζ (2)} = \frac{6}{π^{2}} .$
注: 这并非严格的证明.

A.2.2 一维连续型

1 正态分布

或直接打开网页链接

1.1 基础概念

正态分布又称高斯分布.
$X \sim N(\mu, \sigma^2)$ .
$\displaystyle f(x) = (\sqrt{2\pi}\sigma)\inv \e^{-\tfrac{(x-\mu)^2}{2\sigma^2}}$ .
$Y = (X-\mu)/\sigma \sim N(0,1)$ .
$3\sigma$ 原则: 0.6826，09544，9.9974.
$\alpha$ $\varPhi(z_\alpha) = 1-\alpha$ .
$z_{1-\alpha}$

1.2 数字特征

$\mu$ .
$\sigma^2$ .
$\alpha_2 = E(X^2) = \sigma^2 + \mu^2$ .
$k$ $\mu_k = \begin{cases} \sigma^k(k-1)!!, & k\text{ 为偶数,} \\ 0, & k\text{ 为奇数.} \end{cases}$
$\beta_1 = 0$ .
$\beta_2 = 3$ .
$g(t) = \e^{\i \mu t - \tfrac{\sigma^2}{2} t^2}$ .
$\phi_X(t) = \e^{\tfrac{t^2\sigma^2}{2 n} + \mu t}$ .

1.3 其它性质

$aN(\mu, \sigma^2) + b \sim N(a\mu + b, a^2\sigma^2)$ .
$X$ $Y$ $N(0, 1)$ $(X, Y)$ $(R, \Theta)$ $R$ $\Theta$ 独立.
相互独立的正态分布的函数
- 分布之和
  - $X_1 \sim N(\mu_1, \sigma_1^2),\, X_2 \sim N(\mu_2, \sigma_2^2)$ $X_1 + X_2 \sim N(\mu_1 + \mu_2, \sigma_1^2 + \sigma_2^2)$ .
  - $X_i \sim N(\mu_i, \sigma_i^2)$ $X_1 + \cdots + X_n \sim N(\mu_1 + \cdots + \mu_n, \sigma_1^2 + \cdots + \sigma_n^2)$ .
- 分布之差
  $X_1 \sim N(\mu_1, \sigma_1^2),\, X_2 \sim N(\mu_2, \sigma_2^2)$ $X_1 - X_2 \sim N(\mu_1 - \mu_2, \sigma_1^2 + \sigma_2^2)$ .
- 分布之商
  $X_1$ $X_2$ $N(0, 1)$ $X_1 / X_2 \sim C(1, 0)$ (柯西分布).
- 分布之积
  $X_1 \sim N(0, \sigma_1^2),\, X_2 \sim N(0, \sigma_2^2)$ $X_1X_2 \sim \dfrac{1}{\pi\sigma_1\sigma_2} K_0\pqty{\dfrac{\vqty{z}}{\sigma_1\sigma_2}}$ (修正贝塞尔函数; 暂时未学)
- 平方之和
  $\soneto{X}{n}$ $N(0, 1)$ $Y = X_1^2 + X_2^2 +\cdots + X_n^2 \sim \chi_n^2$ .
统计量的分布
- $\overline{X}$ $S^2 = \dfrac{1}{n-1} \insum (X_i - \overline{X})$ 独立.
- 均值已知, 标准差已知
  - $\overline{X} \sim N\pqty{\mu, \dfrac{\sigma^2}{n}}$ .
  - $\dfrac{\sqrt{n} (\overline{X} - \mu)}{\sigma} \sim N(0, 1)$ .
  - $\insum\pqty{\dfrac{X_i - \mu}{\sigma}}^2 \sim \chi_n^2$ .
- 均值已知, 标准差未知
  - $\dfrac{\sqrt{n}\, (\overline{X} - \mu)}{S} \sim t_{n-1}$ .
- 均值未知, 标准差已知
  - $\dfrac{\mathrm{SS}}{\sigma^2} = \dfrac{(n-1)S^2}{\sigma^2} = \insum \pqty{\dfrac{X_i-\overline{X}}{\sigma}}^2 \sim \chi_{n-1}^2$ .
- 两份相互独立的样本
  $\soneto{X}{n_1},\, \mathrm{iid},\, \sim N(\mu_1, \sigma_1^2)$ .
  $\soneto{Y}{n_2},\, \mathrm{iid},\, \sim N(\mu_2, \sigma_2^2)$ .
  - $\overline{X} - \overline{Y} \sim N\pqty{\mu_1 - \mu_2, \dfrac{\sigma_1^2}{n_1} + \dfrac{\sigma_2^2}{n_2}}$ .
  - $\left. \dfrac{S_1^2}{\sigma_1^2} \right/ \dfrac{S_2^2}{\sigma_2^2} \sim f(n_1-1, n_2-1)$ .
  - $\sigma_1^2 = \sigma_2^2 = \sigma^2$ 时,
    $\begin{aligned} S_{ω} := \sqrt{\frac{(n_{1} - 1) S_{1}^{2} + (n_{2} - 1) S_{2}^{2}}{n_{1} + n_{2} - 2}}, \\ \frac{(\overset{―}{X} - \overset{―}{Y}) - (μ_{1} - μ_{2})}{S_{ω} \sqrt{\frac{1}{n_{1}} + \frac{1}{n_{2}}}} \sim t_{n_{1} + n_{2} - 2} . \end{aligned}$
    $\dfrac{\sqrt{n} (\overline{X} - \mu)}{\sigma}$ $\dfrac{\mathrm{SS}}{\sigma^2}$ , 由 t 分布的定义即得.

1.4 参数估计

$N(\mu, \sigma^2)$ $\mu$ $\sigma^2$ 的估计.
- $\sigma^2$ $\mu$ .
  - $\mu = m$ .
    $\sigma^2$ 是否已知, 均为 MVU 估计.
  - 区间估计 (枢轴变量法)
    $\dfrac{\sqrt{n} (\overline{X} - \mu) } {\sigma} \sim N(0, 1)$ , 知
    $[{\hat{μ}}_{1}, {\hat{μ}}_{2}] = [\overset{―}{X} - \frac{σ}{\sqrt{n}} u_{α / 2}, \overset{―}{X} + \frac{σ}{\sqrt{n}} u_{α / 2}] .$
- $\mu$ $\sigma^2$ .
  - $\hat{\sigma^2} = m_2$ .
    $\mu$ $\dfrac{2}{n}\sigma^4$ .
  - 区间估计 (枢轴变量法)
    $\dfrac{1}{\sigma^2} \insum (X_i - \mu)^2 \sim \chi_n^2$ 知
    $[\hat{σ_{1}^{2}}, \hat{σ_{2}^{2}}] = [\frac{\sum_{i = 1}^{n} (X_{i} - μ)^{2}}{χ_{n}^{2} (\frac{α}{2})}, \frac{\sum_{i = 1}^{n} (X_{i} - μ)^{2}}{χ_{n}^{2} (\frac{α}{2})}] .$
- $\mu$ $\sigma^2$ .
  - 矩估计
    - $\mu = m$ .
      $\sigma^2$ 是否已知, 均为 MVU 估计.
    - $\sigma^2 = S^2$ .
      $\mu$ 未知时的 MVU 估计.
  - 极大似然估计
    - $\mu = m$ . (MVU 估计)
    - $\sigma^2 = m_2$ . (非 MVU 估计)
  - 区间估计 (枢轴变量法)
    - $\dfrac{\sqrt{n}\, (\overline{X} - \mu)}{S} \sim t_{n-1}$ $t$ 区间估计为
      $[{\hat{μ}}_{1}, {\hat{μ}}_{2}] = [\overset{―}{X} - \frac{S}{\sqrt{n}} t_{n - 1} (\frac{α}{2}), \overset{―}{X} + \frac{S}{\sqrt{n}} t_{n - 1} (\frac{α}{2})] .$
    - $\dfrac{(n-1)S^2}{\sigma^2} \sim \chi_{n-1}^2$ , 知
      $[\hat{σ_{1}^{2}}, \hat{σ_{2}^{2}}] = [\frac{(n - 1) S^{2}}{χ_{n - 1}^{2} (\frac{α}{2})}, \frac{(n - 1) S^{2}}{χ_{n - 1}^{2} (1 - \frac{α}{2})}] .$
  - 无偏估计 (通过调整系数而得)
    $\tilde{σ} = \sqrt{\frac{n - 1}{2}} \frac{Γ (\frac{n - 1}{2})}{Γ (\frac{n}{2})} S .$
$N(\mu_1, \sigma_1^2)$ $N(\mu_2, \sigma_2^2)$ $\mu_1 - \mu_2$ $\sigma_1^2 / \sigma_2^2$ 的区间估计.
- $\delta = \mu_1 - \mu_2$ .
  - $\sigma_1^2$ $\sigma_2^2$ 已知.
    $U = \frac{(\overset{―}{X} - \overset{―}{Y}) - (μ_{1} - μ_{2})}{\sqrt{\frac{σ_{1}^{2}}{n_{1}} + \frac{σ_{2}^{2}}{n_{2}}}} \sim N (0, 1),$ $\begin{aligned} [{\hat{δ}}_{1}, {\hat{δ}}_{2}] & = [\overset{―}{X} - \overset{―}{Y} - z_{α / 2} \sqrt{\frac{σ_{1}^{2}}{n_{1}} + \frac{σ_{2}^{2}}{n_{2}}}, \\ \overset{―}{X} - \overset{―}{Y} + z_{α / 2} + \sqrt{\frac{σ_{1}^{2}}{n_{1}} + \frac{σ_{2}^{2}}{n_{2}}}] . \end{aligned}$
  - $\sigma_1^2 = \sigma_2^2 = \sigma^2$ 未知.
    $\begin{matrix} S_{ω}^{2} := \frac{(n_{1} - 1) S_{1}^{2} + (n_{2} - 1) S_{2}^{2}}{n_{1} + n_{2} - 2}, \\ \frac{(\overset{―}{X} - \overset{―}{Y}) - (μ_{1} - μ_{2})}{S_{ω} \sqrt{\frac{1}{n_{1}} + \frac{1}{n_{2}}}} \sim t_{n_{1} + n_{2} - 2}, \end{matrix}$ $\begin{aligned} [{\hat{δ}}_{1}, {\hat{δ}}_{2}] & = [\overset{―}{X} - \overset{―}{Y} - t_{n_{1} + n_{2} - 2} (\frac{α}{2}) S_{ω} \sqrt{\frac{1}{n_{1}} + \frac{1}{n_{2}}}, \\ \overset{―}{X} - \overset{―}{Y} + t_{n_{1} + n_{2} - 2} (\frac{α}{2}) S_{ω} \sqrt{\frac{1}{n_{1}} + \frac{1}{n_{2}}}] . \end{aligned}$
  - $\sigma_1^2$ $\sigma_2^2$ 未知.
    即贝伦斯 - 费歇尔问题, 目前还没有较好的处理方法.
    不过可以利用大样本法, 近似同方差已知的情况处理.
    $\begin{aligned} N (0, 1) & \sim [(\overset{―}{X} - \overset{―}{Y}) - (μ_{1} - μ_{2})] / \sqrt{σ_{1}^{2} / n + σ_{2}^{2} / m} & (严格的) \\ \sim [(\overset{―}{X} - \overset{―}{Y}) - (μ_{1} - μ_{2})] / \sqrt{S_{1}^{2} / n + S_{2}^{2} / m} & (近似的) \end{aligned}$
- $\lambda = \sigma_1^2 / \sigma_2^2$ .
  - $\mu_1$ $\mu_2$ 已知.
    $F = \frac{\sum_{i = 1}^{n_{2}} \frac{(Y_{i} - μ_{2})^{2}}{n_{2} σ_{2}^{2}}}{\sum_{i = 1}^{n_{1}} \frac{(X_{i} - μ_{1})^{2}}{n_{1} σ_{1}^{2}}} \sim F_{n_{2}, n_{1}},$ $\begin{aligned} [{\hat{λ}}_{1}, {\hat{λ}}_{2}] & = [\frac{\sum_{i = 1}^{n_{1}} \frac{(X_{i} - μ_{1})^{2}}{n_{1}}}{\sum_{i = 1}^{n_{2}} \frac{(Y_{i} - μ_{2})^{2}}{n_{2}}} F_{n_{2}, n_{1}} (1 - \frac{α}{2}), \\ \frac{\sum_{i = 1}^{n_{1}} \frac{(X_{i} - μ_{1})^{2}}{n_{1}}}{\sum_{i = 1}^{n_{2}} \frac{(Y_{i} - μ_{2})^{2}}{n_{2}}} F_{n_{2}, n_{1}} (\frac{α}{2})] . \end{aligned}$
  - $\mu_1$ $\mu_2$ 未知.
    $\frac{S_{1}^{2} / σ_{1}^{2}}{S_{2}^{2} / σ_{2}^{2}} \sim F_{n_{1} - 1, n_{2} - 1},$ $[{\hat{λ}}_{1}, {\hat{λ}}_{2}] = [\frac{S_{1}^{2}}{S_{2}^{2}} F_{n_{2} - 1, n_{1} - 1} (1 - α), \frac{S_{1}^{2}}{S_{2}^{2}} F_{n_{2} - 1, n_{1} - 1} (\frac{α}{2})] .$
$\sigma / \mu$ .
- $\sqrt{m_2}/m$ $S/m$ .
$N(\theta, 1)$ $\theta$ .
- $h(\theta) \sim N(\mu, \sigma^2)$ , 则
  $\tilde{\theta} = \dfrac{n}{n+1/\sigma^2} \overline{X} + \dfrac{1/\sigma^2}{n+1\sigma^2} \mu$ .

2 指数分布

或直接打开网页链接

2.1 基础概念

指数分布又称为负指数分布.
$X \sim E(\lambda)$ .
$f(x) = \begin{cases} \lambda\e^{-\lambda x}, & x>0, \\ 0, & x \le 0. \\ \end{cases}$
$F(x) = \begin{cases} 1-\e^{-\lambda x}, & x>0, \\ 0, & x \le 0. \end{cases}$

2.2 数字特征

$E[X] = \lambda\inv$ .
$\Var[X] = \lambda^{-2}$ .
$k$ $E(X^k) = \dfrac{k!}{\lambda^k}$ .
$g(t) = \dfrac{\lambda}{\lambda - \i t}$ .
$m_X(t) = \dfrac{\lambda}{\lambda - t},\, t < \lambda$ .

2.3 其它性质

$aE(\lambda) = E\pqty{\dfrac{\lambda}{a}}$ .
无记忆性 $P(X > m+t \mid X>m) = P(X>t)$ .
$X \sim E(\lambda)$ $T$ $Y \sim P(\lambda T)$ $%先算出 Y=0 的情况, 再用数学归纳法.$
$\soneto{X}{n}$ $E(\lambda)$ , 则
$Y = 2 λ (X_{1} + X_{2} + \dots + X_{n}) \sim χ_{2 n}^{2} .$
$X_i \sim E(\lambda_i)$ 相互独立, 则
$Y = min (X_{1}, X_{2}, \dots, X_{n}) \sim E (λ_{1} + λ_{2} + \dots + λ_{n}) .$

2.4 参数估计

$1 / \lambda = m$ . (MVU 估计)
$\lambda = 1/m$ .
$h(\lambda) = \lambda\e^{-\lambda}\; (\lambda>0)$ $\lambda = \dfrac{n+2}{n\overline{X}+1}$ .
区间估计
- 枢轴变量法
  - $\lambda$ .
    $2n\lambda \overline{X} \sim \chi_{2n}^2$ , 知
    $[{\hat{θ}}_{1}, {\hat{θ}}_{2}] = [χ_{2 n}^{2} (1 - α / 2) / (2 n \overset{―}{X}), χ_{2 n}^{2} (α / 2) / (2 n \overset{―}{X})] .$
  - $1/\lambda$ .
    $2n\lambda \overline{X} \sim \chi_{2n}^2$ , 知
    $[{\hat{θ}}_{1}, {\hat{θ}}_{2}] = [(2 n \overset{―}{X}) / χ_{2 n}^{2} (1 - α / 2), (2 n \overset{―}{X}) / χ_{2 n}^{2} (α / 2)] .$
$\soneto{X}{n}$ $E(\lambda_1)$ $\soneto{Y}{m}$ $E(\lambda_2)$ $\lambda_2 / \lambda_1$ .
- 区间估计 (枢轴变量法)
  - $\dfrac{4\lambda_1 n\overline{X}}{4\lambda_2m\overline{Y}} \sim \dfrac{2n\chi_{2n}^2}{2m\chi_{2m}^2} \sim F_{2n, 2m}$ .

3 混合指数分布

3.1 基础概念

混合指数分布又称为 超指数分布 (Hyperexponential Distribution).
$m$ $X_i \sim E(\lambda_i)$ $p_i$ $i$ $m$ 阶超指数分布.
$f(x) = \dsum_{i=1}^m p_i \lambda_i \e^{-\lambda_i x},\quad (x>0)$ .
$\dsum_{i=1}^m p_i = 1$ .
$F(x) = \dsum_{i=1}^m p_i \pqty{1 - \e^{-\lambda_i x}},\quad (x>0)$ .

3.2 数字特征

和指数分布一样, 不再赘述. 如
$k$ $E(X^k) = \dsum_{i=1}^m \dfrac{k!}{\lambda_i^k} p_i$ .

3.3 其它性质

无记忆性.
$p_i = \dfrac{1}{m},\, i = \oneto{m}$ $X \sim \chi_{2m}^2$ .

3.4 参数估计

4 均匀分布

4.1 基础概念

$X \sim R(a, b)$ .
$f(x) = \begin{cases} 1/(b-a), & a \le x \le b, \\ 0, & x<a \;或\; x>b. \end{cases}$
$F(x) = \begin{cases} 0, & x \le a, \\ (x-a)/(b-a), & a<x<b, \\ 1, & x \ge b. \end{cases}$

4.2 数字特征

$\dfrac{a+b}{2}$ .
$\dfrac{(b-a)^2}{12}$ .
$k$ $\alpha_k = \dfrac{1}{k+1} \dfrac{b^{k+1}-a^{k+1}}{b-a}$ .
$k$ $\mu_k = \begin{cases} \dfrac{1}{k+1} \pqty{\dfrac{b-a}{2}}^k, & k \text{ 为偶数,} \\ 0, & k \text{ 为奇数.} \end{cases}$
$\beta_1 = 0$ .
$\beta_2 = \dfrac{9}{5}$ .
$g(t) = \begin{cases} \dfrac{\e^{\i bt} - \e^{\i at}}{\i t(b-a)}, & t \ne 0, \\ 1, & t = 0. \end{cases}$

4.3 其它性质

$cR(a, b) + d \sim R(ac + d, bc + d)\ (c > 0)$ .
$\soneto{X}{n}$ $U(a, b)$ , 则
$\begin{aligned} max (X_{1} + X_{2} + \dots + X_{n}) \sim f (x) = \frac{n (x - a)^{n - 1}}{(b - a)^{n}} \\ min (X_{1} + X_{2} + \dots + X_{n}) \sim f (x) = \frac{n (b - x)^{n - 1}}{(b - a)^{n}} \end{aligned}$
$X \sim U\pqty{-\dfrac{\pi}{2}, \dfrac{\pi}{2}}$ $\tan X \sim C(1, 0)$ .

4.4 参数估计

$R(\theta_1, \theta_2)$ 的参数.
- $\theta_1 = m - \sqrt{3m_2},\, \theta_2 = m + \sqrt{3m_2}$ .
- $\theta_1 = \min\limits_i(X_i),\, \theta_2 = \max\limits_i(X_i)$ .
$R(0, \theta)$ 的参数.
- $\hat{\theta} = \max\limits_{i}(X_i)$ .
- 无偏估计
  - $\hat{\theta} = \dfrac{n+1}{n} \max\limits_i(X_i)$ . (MVU 估计, 也是相合估计)
  - $\hat\theta = (n+1) \min\limits_i(X_i)$ . (方差很大)
  - $\hat\theta = \max\limits_i(X_i) + \min\limits_i(X_i)$ .
- 区间估计
  - $\hat\theta_1 := \max\limits_i(X_i) \sim F_{\hat\theta_1}(x) = \dfrac{nx^{n-1}}{\theta^n}$ ,
    $[\max(X_i), (1-\alpha)^{-\tfrac{1}{n}} \max(X_i)]$ $1-\alpha$ .

5 对数正态分布

或直接打开网页链接

5.1 基础概念

$\ln{X} \sim N(\mu, \sigma^2)$ .
$f(x, \mu, \sigma) = \begin{cases} \pqty{x\sqrt{2\pi}\sigma}\inv \exp\bqty{ -\dfrac{(\ln{x}-\mu)^2}{2\sigma^2} }, & x>0, \\ 0, & x \le 0. \end{cases}$

5.2 数字特征

$E(X) = \e^{\mu + \sigma^2/2}$ .
$\Var(X) = \pqty{\e^{\sigma^2}-1} \e^{2\mu+\sigma^2} = \pqty{\e^{\sigma^2}-1} E(X)^2$ .
$k$ $\alpha_k = \e^{\mu k + k^2\sigma^2/2}$ .
$\beta_1 = \dfrac{\mu_3}{\sigma^3} = \dfrac{\e^{2\sigma^2} - 3\e^{\sigma^2} + 1}{\pqty{\e^{2\sigma^2} - 1}^{3 / 2}}$ .
$\beta_2 = \dfrac{\mu_4}{\sigma^4} = \pqty{\e^{\sigma^2} - 1} \pqty{\e^{4\sigma^2} + 2\e^{3\sigma^2} + 3\e^{2\sigma^2} - 3} \gt 0$ .

5.3 其它性质

$\ln bX^a \sim N(a\mu + \ln b, a^2\sigma^2)$ .
对数正态分布总是右偏的.
对数正态分布的期望和方差都是两个参数的增函数.
$\sigma$ $\mu$ 无关.
$\lim\limits_{\sigma \to 0+} E(X) = \e^\mu$ .
$\lim\limits_{\sigma \to 0+} \Var(X) = 0$ .
$\mu=0$ $E(X^k) = E(X)^{k^2}$ .

5.4 参数估计

矩估计
- $\hat{\sigma^2} = \ln\pqty{1 + \dfrac{S^2}{\overline{X}^2}}$ .
- $\hat\mu = 2\ln\overline{X} - \dfrac{1}{2} \ln\pqty{\overline{X}^2 + S^2}$ .

6 柯西分布

或直接打开网页链接

6.1 基础概念

$X \sim C(\gamma, x_0)$ .
$f(x; x_0, \gamma) = \dfrac{1}{\pi} \cdot \dfrac{\gamma}{(x-x_0)^2 + \gamma^2}\quad (-\infty < x < +\infty)$ .
$F(x; x_0, \gamma) = \dfrac{1}{\pi} \arctan\dfrac{x-x_0}{\gamma} + \dfrac{1}{2}$ .
$C(1, 0) \sim t_1$ .
$X_k \sim f_m(X_k \mid \sigma_X) = \dfrac{a_m}{1 + \pqty{\cfrac{X_k^2}{2\sigma_k^2}}^m}\; (a_m > 0.5)$ .

6.2 数字特征

数学期望不存在. (仅 Cauchy 主值积分存在)
方差不存在.
高阶矩不存在.

6.3 其它性质

$X_i$ $C(\gamma, x_0)$ $\splus{X}{n} \sim C(n\gamma, n x_0)$ .
$X_1$ $X_2$ $N(0, 1)$ $\dfrac{X_1}{X_2} \sim C(1, 0)$ .
$X \sim U\pqty{-\dfrac{\pi}{2}, \dfrac{\pi}{2}}$ $\tan X \sim C(1, 0)$ .

6.4 参数估计

$\tilde{m}$ 估计.

7 拉普拉斯分布

或直接打开网页链接

7.1 基础概念

$X \sim \text{La}(\mu, \lambda)$ .
$f(x) = \dfrac{1}{2\lambda}\e^{-\tfrac{\vqty{x-\mu}}{\lambda}}$ .
$F(x) = \begin{cases} \dfrac{1}{2} \e^{\tfrac{x - \mu}{\lambda}}, & x < \mu. \\ 1 - \dfrac{1}{2} \e^{\tfrac{\mu - x}{\lambda}}, & x \ge \mu. \end{cases}$
参数说明
- $\mu$ 是位置参数.
- $\gamma$ 是尺度参数, 越小曲线越陡.
- $\mu = 0$ $E\pqty{\lambda\inv}$ 概率密度的一半.

7.2 数字特征

矩及相关量
- $k$ $\mu_k = E[(X-\mu)^k] = \begin{cases} 0, & k\ 为奇数, \\ k!\lambda^k, & k\ 为偶数. \end{cases}$
- $E(X) = \mu$ .
- $\Var(X) = 2\lambda^2$ .
$k$ 阶中心距、期望和方差比较)
- $E(\vqty{X - \mu}^k) = k!\lambda^k$ .
- $E(\vqty{X - \mu}) = \lambda$ .
- $\Var(\vqty{X - \mu}) = \lambda^2$ .
一些系数
- $\beta_1 = \dfrac{\mu_3}{\sigma^3} = 0$ .
- $\beta_2 = \dfrac{\mu_4}{\sigma^4} = 6$ .
相关函数
- $m(t) = \dfrac{\e^{\tfrac{\mu t}{\lambda}}}{1 - \lambda^2 t^2}$ .
- $g(t) = E(\e^{\i t X}) = \dfrac{\e^{\tfrac{\i\mu t}{\lambda}}}{1 + \lambda^2 t^2}$ .

7.3 其它性质

$a\mathrm{La}(\mu, \lambda) + b \sim \mathrm{La}(a\mu + b, a\lambda)$ .
$\mathrm{La}(\mu, \lambda) \sim \lambda \mathrm{La}(0, 1) + \mu$ .
注意到 Laplace 分布与指数分布的关系, 可以立即得到如下平凡的结论
- $X \sim \mathrm{La}(\alpha, \beta)$ $\dfrac{2}{\beta} \vqty{X - \alpha} \sim \chi_2^2 \sim \Gamma(1, 2)$ .
- $X$ $Y$ $\mathrm{La}(\alpha, \beta)$ $\dfrac{\vqty{X - \alpha}}{\vqty{Y - \alpha}} \sim F_{2, 2}$ .
- $X_{11}, X_{12}, X_{21}, X_{22}$ $N(0, 1)$ $D = \begin{vmatrix} X & Y \\ Z & W \end{vmatrix} \sim \mathrm{La}(0, 2)$ .
与稳健性的联系
古典回归分析中, 用偏差平方和的大小作为标准, 这种回归不具有稳健性.
而改成偏差的绝对值和作为标准, 却具有稳健性 (尽管求解更加困难).
标准 Laplace 分布
- $\mathrm{La}(x; 0, 1) = \dfrac{\e^{-\vqty{x}}}{2}$ .
- $\phi_L(t) = \dfrac{1}{1 + t^2}$ .

7.4 参数估计

$\mu$ .
- $\hat\mu = \overline{X}$ .
- $\hat\mu = m_e$ (中位数).
$\lambda$ .
- $\hat\lambda = \dfrac{\sqrt2}{2} S$ (标准差).
- 类似矩估计的估计:
  $\hat{λ} = \frac{1}{n} \sum_{i = 1}^{n} | X_{i} - μ | \approx \frac{1}{n} \sum_{i = 1}^{n} | X_{i} - \hat{μ} | .$

8 卡方分布

或直接打开网页链接

8.1 基础概念

$n$ $X \sim \chi_n^2$ .
概率密度函数
$\begin{matrix} k_{n} (x) = {\begin{cases} \frac{e^{- \frac{x}{2}} x^{\frac{n}{2} - 1}}{Γ (\frac{n}{2}) 2^{\frac{n}{2}}}, & x > 0, \\ 0, & x \leq 0. \end{cases} \end{matrix}$
$x>0$ )
$\begin{array}{ll} k_{1} (x) = \frac{e^{- \frac{x}{2}}}{\sqrt{2 π x}} & k_{2} (x) = \frac{1}{2} e^{- \frac{x}{2}} \\ k_{3} (x) = \frac{\sqrt{x} e^{- \frac{x}{2}}}{\sqrt{2 π}} & k_{4} (x) = \frac{x}{4} e^{- \frac{x}{2}} \end{array}$
$\alpha$ $\chi_\alpha^2(n)$ .
$X \sim \chi_n^2$ ,
$\frac{X - n}{\sqrt{2 n}} \dot{\sim} N (0, 1) \Rightarrow \frac{χ_{α}^{2} (n) - n}{\sqrt{2 n}} \approx z_{α} \Rightarrow χ_{α}^{2} (n) \approx n + z_{α} \sqrt{2 n} .$

8.2 数字特征

$E(X) = n$ .
$\Var(X) = 2n$ .
注意到方差是均值的两倍，可以以此检验是否为卡方分布.
$E(X\inv) = \dfrac{1}{n-2}$ .
$E(X^k) = \dfrac{2^k\, \Gamma\pqty{\cfrac{n}{2}+k}}{\Gamma\pqty{\cfrac{n}{2}}} = 2^k \pqty{\dfrac{n}{2}}^{(k)} %\ \pqty{k > -\dfrac{n}{2}}$ .
$g(t) = \dfrac{1}{(1 - 2\i t)^{\tfrac{n}{2}}}$ .
$m_X(t) = \dfrac{1}{(1 - 2t)^{\tfrac{n}{2}}}, \quad t < \dfrac{1}{2}$ .

8.3 其它性质

$\soneto{X}{n}$ $N(0, 1)$ , 则
$Y = X_{1}^{2} + X_{2}^{2} + \dots + X_{n}^{2} \sim χ_{n}^{2} .$
$X_1 \sim \chi_m^2$ $X_2 \sim \chi_n^2$ 独立, 则
$X_{1} + X_{2} \sim χ_{m + n}^{2} .$
$\soneto{X}{n}$ $E(\lambda)$ , 则
$X = 2 λ (X_{1} + X_{2} + \dots + X_{n}) \sim χ_{2 n}^{2} .$
$\soneto{X}{n}$ $N(\mu, \sigma^2)$ , 则
$\frac{SS}{σ^{2}} = \frac{(n - 1) S^{2}}{σ^{2}} \sim χ_{n - 1}^{2} .$

9 t 分布

或直接打开网页链接

9.1 基础概念

$n$ $X \sim t_n$ .
概率密度函数
$\begin{aligned} t_{n} (x) & = \frac{Γ (\frac{n + 1}{2})}{\sqrt{n π} Γ (\frac{n}{2})} {(1 + \frac{x^{2}}{n})}^{- \frac{n + 1}{2}} = \frac{{(1 + \frac{x^{2}}{n})}^{- \frac{n + 1}{2}}}{B (\frac{n}{2}, \frac{1}{2}) \sqrt{n}}, - \infty < x < + \infty . \end{aligned}$
$\alpha$ $t_\alpha(n) \approx z_\alpha$ $\alpha$ 分位数)
$t_{1 - \alpha}(n) = - t_\alpha(n)$ .

9.2 数字特征

$E(t_n) = 0\; (n>1)$ .
$\Var(t_n) = \dfrac{n}{n-2}\; (n>2)$ .
$E(X^k) = \dfrac{\Beta\pqty{\cfrac{n-k}{2}, \cfrac{k+1}{2}}}{\Beta\pqty{\cfrac{n}{2}, \cfrac{1}{2}}} n^{\tfrac{k}{2}}\ (-1 < k < n)$ .

9.3 其它性质

$X \sim t_n$ $X^2 \sim F_{1, n}$ .
$X \sim N(0, 1)$ $Y \sim \chi_n^2$ 独立, 则
$\frac{X}{\sqrt{Y / n}} \sim t_{n} .$
$\soneto{X}{n}$ $N(\mu, \sigma^2)$ , 则
$\frac{\overset{―}{X} - μ}{S / \sqrt{n}} \sim t_{n - 1} .$
$\soneto{X}{n}$ $N(\mu_1, \sigma^2)$ $\soneto{Y}{m}$ $N(\mu_2, \sigma^2)$ $X_i, Y_j$ 独立, 则
$\frac{\sqrt{\frac{n m (n + m - 2)}{n + m}} [(\overset{―}{X} + \overset{―}{Y}) - (μ_{1} - μ_{2})]}{\sqrt{\sum_{i = 1}^{n} (X_{i} - \overset{―}{X})^{2} + \sum_{j = 1}^{m} (Y_{j} - \overset{―}{Y})^{2}}} \sim t_{n + m - 2} .$

10 F 分布

或直接打开网页链接

10.1 基础概念

$(m, n)$ $X \sim F_{m, n}$ .
概率密度函数
$\begin{aligned} f_{m, n} (x) & = \frac{m^{\frac{m}{2}} n^{\frac{n}{2}} x^{\frac{m}{2} - 1} I_{{x \geq 0}}}{B (\frac{m}{2}, \frac{n}{2}) (m x + n)^{\frac{m + n}{2}}} \\ = \frac{{(\frac{m}{n})}^{\frac{m}{2}} x^{\frac{m}{2} - 1} I_{{x \geq 0}}}{B (\frac{m}{2}, \frac{n}{2}) {(1 + \frac{m}{n} x)}^{\frac{m + n}{2}}} . \end{aligned}$
$F \sim F(m, n)$ $F\inv \sim F(n, m)$ .
$n_1$ $n_2$ $F$ $\alpha$ $F_\alpha(n_1, n_2)$ .
$F_\alpha(m, n) \cdot F_{1-\alpha}(n, m) = 1$ .

10.2 数字特征

$E(f_{m,n}) = \dfrac{n}{n-2}\; (n>2)$ .
$\Var(f_{m,n}) = \dfrac{2n^2(m+n-2)}{m(n-2)^2(n-4)}$ .
$E(X^k) = \dfrac{ \Beta\pqty{ \cfrac{m}{2} + k, \cfrac{n}{2} - k } }{ \pqty{\cfrac{m}{n}}^k \Beta\pqty{ \cfrac{m}{2}, \cfrac{n}{2} } }$ .

10.3 其它性质

$X_1, X_2$ $X_1 \sim \chi_m^2,\, X_2 \sim \chi_n^2$ , 则
$\frac{X_{1}}{m} / \frac{X_{2}}{n} \sim F_{m, n} .$
$\soneto{X}{n}$ $N(\mu_1, \sigma_1^2)$ $\soneto{Y}{m}$ $N(\mu_2, \sigma_2^2)$ $X_i, Y_j$ 独立, 则
$\frac{S_{Y}}{σ_{2}^{2}} / \frac{S_{X}}{σ_{1}^{2}} \sim F_{m - 1, n - 1} .$
$\forall k, n, \in \N, a \in (0, 1): kF_{k, n}(a) \ge F_{1, n}(a)$ $%利用定义, 见习题 29.$

11 贝塔分布

或直接打开网页链接

11.1 基础概念

$X \sim \mathrm{Be}(\alpha, \beta) \quad (\alpha, \beta > 0)$ .
$f(x; \alpha, \beta) = \dfrac{x^{\alpha - 1} (1-x)^{\beta - 1}}{\Beta(\alpha, \beta)}\quad (0 < x < 1)$ .
$F(x; \alpha, \beta) = \dfrac{\Beta_x(\alpha, \beta)}{\Beta(\alpha, \beta)} = I_x(\alpha, \beta)$ .
- $\Beta_x(\alpha, \beta)$ .
- $I_x(\alpha, \beta)$ .

11.2 数字特征

常用统计量
- $M_0 = \dfrac{\alpha - 1}{\alpha + \beta - 2}$ . (伯努利分布参数的极大似然估计)
- $E(X) = \dfrac{\alpha}{\alpha + \beta}$ . (伯努利分布参数的贝叶斯估计 & 同等无知原则)
- $\Var(X) = \dfrac{\alpha\beta}{(\alpha + \beta)^2 (\alpha + \beta + 1)}$ .
矩及相关量
- $k$ $E(X^k) = \dfrac{\Beta(\alpha + k, \beta)}{\Beta(\alpha, \beta)} = \dfrac{(\alpha)^{(k)}}{(\alpha + \beta)^{(k)}} = \dfrac{\alpha + k - 1}{\alpha + \beta + k - 1} E(X^{k-1})$ .
- $\beta_1 = \dfrac{\mu_3}{\sigma^3} = \dfrac{2(\beta - \alpha) \sqrt{\alpha + \beta + 1}}{(\alpha + \beta + 2) \sqrt{\alpha \beta}}$ .
- $\beta_2 = \dfrac{\mu_4}{\mu_2^2} - 3 = \dfrac{6[(\alpha - \beta)^2 (\alpha + \beta + 1) - \alpha \beta (\alpha + \beta + 2)]}{\alpha \beta (\alpha + \beta + 2)(\alpha + \beta + 3)}$ .

11.3 其它性质

Beta 分布即伯努利分布的共轭先验分布.
$E(\ln X) = \psi(\alpha) - \psi(\alpha + \beta)$ .
- $\Beta_{p, q}(\alpha, \beta) := \dfrac{\partial^{p+q}\Beta(x, y)}{\partial^p x \partial^q y} = \dint_0^1 x^{\alpha - 1} (1-x)^{\beta - 1} \ln^p x \ln^q(1-x) \dx$ .
- $\Beta_{1, 0}(x, y) = \Beta(x, y) (\psi(x) - \psi(x+y))$ .
- $\Beta_{0, 1} (x, y) = \Beta(x, y) (\psi(y) - \psi(x + y))$ .
Beta 分布与 Gamma 分布的关系.

12 伽马分布

或直接打开网页链接

12.1 基础概念

$X \sim \mathrm{Ga}(\alpha, \beta) \sim \Gamma\pqty{\alpha, \dfrac{1}{\beta}}$ .
$f(x; \alpha, \beta) = \dfrac{\beta^\alpha}{\Gamma(\alpha)} x^{\alpha - 1} \e^{-\beta x} \quad (x > 0)$ .
- $\alpha$ 称为形状参数.
- $\beta$ 称为逆尺度参数.
$F(x; \alpha, \beta) = \dfrac{\gamma(\alpha, \beta x)}{\Gamma(\alpha)}$ .
- $\gamma(s, x) = \dint_0^x t^{s-1} \e^{-t} \dt$ 为下不完全 Gamma 函数.
- $\Gamma(s, x) = \dint_x^{+\infty} t^{s-1} \e^{-t} \dt$ 为上不完全 Gamma 函数.
注意区分
- $\mathrm{Ga}(\alpha, \beta)$ $\mathrm{Gamma}(\alpha, \beta)$ , 其累积分布函数如上所示.
- 另一种定义 $\Gamma(\alpha, \beta)$ $\dfrac{\gamma(\alpha, x / \beta)}{\Gamma(\alpha)}$ .
- $\Gamma(x; \alpha, \beta)$ $\Gamma(X \mid \alpha, \beta)$ .
- $\Gamma(s, x)$ $\Gamma(s)$ .
$\alpha \in \N$ 时, 退化为埃尔朗分布.

12.2 数字特征

有量纲参数
- $M_0 = \dfrac{\alpha - 1}{\beta}\quad (\alpha > 1)$ .
- $k$ $\alpha_k = E(X^k) = \dfrac{\Gamma(\alpha + k)}{\beta^k \Gamma(\alpha)} = \dfrac{(\alpha)^{(k)}}{\beta^k}$ . (上升阶乘幂)
- $\mu = E(X) = \dfrac{\alpha}{\beta}$ .
- $\sigma^2 = \Var(X) = \dfrac{\alpha}{\beta^2}$ .
无量纲参数
- $\beta_1 = \dfrac{\mu_3}{\sigma^3} = \dfrac{2}{\sqrt{\alpha}}$ .
- $\beta_2 = \dfrac{\mu_4}{\sigma^4} = \dfrac{6}{\alpha}$ .
- $c_v = \dfrac{\sigma}{\mu} = \dfrac{1}{\sqrt{\alpha}}$ .
$g(t) = \pqty{1 - \dfrac{\i t}{\beta}}^{-\alpha}$ .
$m_X(t) = m_X(t) = \pqty{ 1 - \dfrac{t}{\beta} }^{-\alpha},\, t < \beta$ .

12.3 其它性质

变化趋势
- $\alpha \in (0, 1]$ $f(x; \alpha, \beta)$ 递减.
- $\alpha \in (1, +\infty)$ $f(x; \alpha, \beta)$ 先增后减, 为单峰函数.
- $\alpha$ $\alpha$ 称为形状参数.
特殊情况
- $\mathrm{Ga}(1, \lambda) \sim E(\lambda)$ .
  $\Gamma\pqty{1, \dfrac{1}{\lambda}} \sim E(\lambda)$ $\Gamma(1, \lambda) \sim E(\lambda)$ , 问就是别用)
- $\mathrm{Ga}\pqty{\dfrac{n}{2}, \dfrac{1}{2}} \sim \chi_n^2$ .
  $\Gamma\pqty{\dfrac{n}{2}, 2} \sim \chi_n^2$ .
函数运算
- 数乘
  - $X \sim \mathrm{Ga}(\alpha, \beta)$ $\lambda X \sim \mathrm{Ga}\pqty{\alpha, \dfrac{\beta}{\lambda}}$ .
  - $\beta$ $\beta$ 越大, 曲线越窄, 图像越接近 y 轴.
- 可加性
  - $X_1 \sim \mathrm{Ga}(\alpha_1, \beta)$ $X_2 \sim \mathrm{Ga}(\alpha_2, \beta)$ $X + Y \sim \mathrm{Ga}(\alpha_1 + \alpha_2, \beta)$ .
  - $X_m \sim \chi_m^2,\, X_n \sim \chi_n^2$ $\chi_m^2 + \chi_n^2 \sim \chi_{m+n}^2$ .
  - $X_i$ $N(0, 1)$ $\splus{X^2}{n} \sim \chi_n^2$ .
  - $X_i$ $E(\lambda)$ $2\lambda(\splus{X}{n}) \sim \chi_{2n}^2$ .

13 威布尔分布

或直接打开网页链接

13.1 基础概念

$f(x; \lambda, k) = \begin{cases} \dfrac{k}{\lambda} \pqty{ \dfrac{x}{\lambda} }^{k - 1} \e^{ -\pqty{ \tfrac{x}{\lambda} }^k}, & x \ge 0, \\ 0, & x < 0. \end{cases}$
$F(x) = \begin{cases} 1 - \e^{- \pqty{ \tfrac{x}{\lambda} }^k}, & x \ge 0, \\ 0, & x \le 0. \\ \end{cases}$

13.2 数字特征

$n$ $E(X^n) = \lambda^n \Gamma\pqty{1 + \dfrac{n}{k}}$ .
期望、方差、偏度、峰度等可由原点矩直接得到, 形式复杂故不再列出.

14 瑞利分布

14.1 基础概念

$f(x) = \dfrac{x}{\sigma^2} \e^{-\tfrac{x^2}{2\sigma^2}},\quad x > 0$ .
$F(x) = 1 - \e^{-\tfrac{x^2}{\lambda^2}},\quad x > 0$ .

14.2 数字特征

$k$ $E(X^k) = (2\sigma^2)^k \Gamma\pqty{1 + \dfrac{k}{2}}$ .
$E(X) = \sqrt{\dfrac{\pi}{2}} \sigma \approx 1.253 \sigma$ .
$\Var(X) = \dfrac{4 - \pi}{2} \sigma^2 \approx 0.429 \sigma^2$ .

15 帕累托分布

15.1 基础概念

帕累托分布 (Pareto Distribution) 又称布拉德福分布, 与幂律分布形式相同. 参考齐夫定律.
$f(x) = \begin{cases} 0, & x < x_{\min}, \\ \dfrac{k x_\min^k}{x^{k+1}}, & x \ge x_{\min}. \end{cases}$
$P(X>x) = \begin{cases} 0, & x < x_\min, \\ \pqty{\dfrac{x_\min}{x}}^k, & x \ge x_\min. \\ \end{cases}$
互补累积分布函数又称为生存函数, 残存函数 或可靠性函数.
大致服从帕累托分布的例子
- 个人财富或资源的分布.
- 人类居住区的大小.
- 对百科条目的访问.
- 龙卷风带来的灾难的数量.

15.2 数字特征

$f(x) = \dfrac{\alpha \theta^\alpha}{x^{\alpha + 1}},\, x \ge \theta$ .
$k$ $E(X^k) = \dfrac{\alpha \theta^k}{\alpha - k},\, (\alpha > k)$ .
$E(X) = \dfrac{\alpha \theta}{\alpha - 1},\, (\alpha > 1)$ .
$\Var(X) = \dfrac{\alpha \theta^2}{(\alpha-1)^2 (\alpha - 2)},\, (\alpha > 2)$ .

16 逻辑斯蒂分布

16.1 基础概念

$X \sim L(\mu, \gamma)$ .
Logistic 分布属于位置-尺度参数族.
$F(x) = \dfrac{1}{ 1 + \e^{ -\tfrac{x - \mu}{\gamma} } } = \dfrac{1}{2} \pqty{ 1 + \tanh \dfrac{x - \mu}{2\gamma} },\quad x \in \R,\, \gamma > 0$ .
$f(x) = \dfrac{ \e^{-\tfrac{x - \mu}{\gamma}} }{ \gamma \pqty{ 1 + \e^{-\tfrac{x - \mu}{\gamma}} }^2 }$ .
参数说明
- $\mu$ 是位置参数, 称为 散布中心.
- $\gamma$ 是尺度参数, 称为 散布程度.
- $\mu = 0$ $\gamma = \pm \gamma_0$ 的分布相同.
$L(0, 1)$ .
- $F_0(x) = \dfrac{1}{1 + \e^{-x}}$ .
- $f_0(x) = \dfrac{\e^{-x}}{(1 + \e^{-x})^2}$ .

16.2 数字特征

$E(X) = \mu$ .
$\Var(X) = \dfrac{\gamma^2\pi^2}{3}$ .

16.3 其它性质

$a L(\mu, \gamma) + b \sim L(a\mu + b, a\gamma)$ .
$L(\mu, \gamma) \sim \gamma L(0, 1) + \mu$ .
$F(\mu - x) + F(\mu + x) = 1$ .
回归模型:
$P_{i} = \frac{1}{1 + e^{- (a + b x_{i})}} \Rightarrow \ln (\frac{P_{i}}{1 - P_{i}}) = a + b x_{i} .$
$y = (1 + \e^{- \bm \beta \bm x})\inv$ .

17 广义贝塔分布

不贴 Geogebra 图像的链接了, 给个 mathematica 绘图代码:


1
\[Alpha] = 2; \[Beta] = 1; \[Gamma] = 3; \[Lambda] = 0.5;
2
Plot[(
3
    \[Lambda]^\[Alpha] \[Beta])
4
    x^(\[Alpha] - 1
5
) / (
6
    Beta[
7
        \[Gamma] - \[Alpha] / \[Beta],
8
        \[Alpha] / \[Beta]
9
    ] (
10
        1 + (\[Lambda] x)^\[Beta]
11
    )^\[Gamma]
12
), {x, 0, 10}]

17.1 基础概念

$X \sim \mathrm{GBeta}(\alpha, \beta, \gamma, \lambda)$ . (随便命的名, 不知道有没有人研究过这东西)
参数定义域
- $\lambda > 0$ .
- $\gamma > \dfrac{\alpha}{\beta} > 0$ .
概率密度函数
$f (x; α, β, γ, λ) = \frac{λ^{α} | β |}{B (γ - \frac{α}{β}, \frac{α}{β})} \frac{x^{α - 1}}{[1 + (λ x)^{β}]^{γ}} I_{{x \geq 0}} .$
$I_\Bqty{x \ge 0} = \begin{cases} 1, & x \ge 0, \\ 0, & x < 0 \end{cases}$
$t = \dfrac{\lambda x}{1 + \lambda x}$ $\intoi f \dx = 1$ .

17.2 数字特征

$E(X^k) = \dfrac{ \Beta\pqty{ \gamma - \cfrac{\alpha + k}{\beta}, \cfrac{\alpha + k}{\beta} } }{ \lambda^k \Beta\pqty{ \gamma - \cfrac{\alpha}{\beta}, \cfrac{\alpha}{\beta} } } = \lambda^{-k} \pqty{ \gamma - \dfrac{\alpha}{\beta} }^{ \pqty{\tfrac{k}{\beta}} } \pqty{ \dfrac{\alpha}{\beta} }^{ \pqty{\tfrac{k}{\beta}} }$ .
$(\alpha)^{(\beta)} = \dfrac{\Gamma(\alpha + \beta)}{\Gamma(\alpha)}$ .

17.3 其它性质

$k$ 阶矩)
- $X \sim \mathrm{GBeta}\pqty{x;1, 2, \dfrac{n + 1}{2}, \dfrac{1}{\sqrt n}}$ $\vqty{X} \sim t_n$ .
- $X \sim \mathrm{GBeta}\pqty{\dfrac{m}{2}, 1, \dfrac{m + n}{2}, \dfrac{m}{n}}$ $X \sim F_{m, n}$ .

其它分布

超指数分布
Dirichlet 分布
广义 Dirichlet 分布
组合 Dirichlet 分布
刘维尔分布
威布尔分布
埃尔朗分布
帕累托分布

A.2.3 多维离散型

1 多项分布

$X = (X_1, \cdots, X_n) \sim M(N; p_1, \cdots, p_n)$ .

P (X_{1} = k_{1}, X_{2} = k_{2}, \dots, X_{n} = k_{n}) = \frac{N!}{k_{1}! k_{2}! \dots k_{n}!} p_{1}^{k_{1}} p_{2}^{k_{2}} \dots p_{n}^{k_{n}} .

多项分布的边缘分布是二项分布.

$(\soneto{X}{n}) \sim M(N; \soneto{p}{n}) \QRA X_1+X_2 \sim B(N;p_1+p_2)$ .

A.2.4 多维连续型

1 矩形均匀分布

2 二维正态分布

2.1 基础概念

$X = (X_1, X_2) \sim N(\mu_1, \mu_2, \sigma_1^2, \sigma_2^2, \rho)$ .

f (x_{1}, x_{2}) = (2 π σ_{1} σ_{2} \sqrt{1 - ρ^{2}})^{- 1} \exp [- \frac{1}{2 (1 - ρ^{2})} (\frac{(x_{1} - μ_{1})^{2}}{σ_{1}^{2}} - \frac{2 ρ (x_{1} - μ_{1}) (x_{2} - μ_{2})}{σ_{1} σ_{2}} + \frac{(x_{2} - μ_{2})^{2}}{σ_{2}^{2}})] .

$\rho=0$ $X_1$ $X_2$ 独立.
$X_1 \sim N(\mu_1, \sigma_1^2),\, X_2 \sim N(\mu_2, \sigma_2^2)$ .

2.2 数字特征

$\Corr(X_1, X_2) = \rho$ .
$\Cov(X_1, X_2) = \rho \sigma_1 \sigma_2$ .
$E(X_1X_2) = \Cov(X_1, X_2) + E(X_1) E(X_2) = \rho \sigma_1 \sigma_2 + \mu_1 \mu_2$ .

2.3 其它性质

二维正态分布的边缘分布是正态分布.
二维正态分布的条件分布是正态分布.
$(X, Y) \sim N(a, b, \sigma_1^2, \sigma_2^2, \rho)$ $X=x$ $Y$ 的条件分布为
$N (b + ρ σ_{2} σ_{1}^{- 1} (x - a), σ_{2}^{2} (1 - ρ^{2})) .$
二维正态分布的边缘分布的和仍为正态分布
$(X_1, X_2) \sim N(\mu_1, \mu_2, \sigma_1^2, \sigma_2^2, \rho)$ $Y = X_1 + X_2 \sim N(\mu_1 + \mu_2, \sigma_1^2 + \sigma_2^2 + 2\rho\sigma_1\sigma_2)$ .
独立的正态分布的联合分布是正态分布.
正态分布的联合分布不一定是二维正态分布.
$Y = X_1 + X_2$ $X_1, X_2$ $X_1, X_2$ 也是正态分布. ⭐️

3 多元正态分布

3.1 基础概念

$(\soneto{X}{n})$ $n$ 元随机变量, 令
$x = (\begin{matrix} x_{1} \\ x_{2} \\ ⋮ \\ x_{n} \end{matrix}), μ = (\begin{matrix} μ_{1} \\ μ_{2} \\ ⋮ \\ μ_{n} \end{matrix}), C = (\begin{matrix} c_{11} & c_{12} & \dots & c_{1 n} \\ c_{21} & c_{22} & \dots & c_{n n} \\ ⋮ & ⋮ & ⋮ \\ c_{n 1} & c_{n 2} & \dots & n_{n n} \end{matrix}),$
$\bm C$ 协方差矩阵 $c_{ij} = \Cov(X_i, X_j) = \rho_{ij} \sigma_i \sigma_j$ .
$(\soneto{X}{n})$ 的概率密度函数为
$f (x_{1}, x_{2}, \dots, x_{n}) = \frac{e^{- \frac{1}{2} (x - μ)^{T} C^{- 1} (x - μ)}}{(2 π)^{\frac{n}{2}} {| C |}^{\frac{1}{2}}}$
$(\soneto{X}{n})$ $\bm \mu,\, \bm C$ $n$ 元正态变量.

3.2 数字特征

$\Var(X_i) = c_{ii}$ .
$\Cov(X_i, X_j) = c_{ij}$ .
$\Corr(X_i, X_j) = \rho_{ij} = \dfrac{c_{ij}}{\sqrt{c_{ii} c_{jj}}}$ .
$E(X_iX_j) = c_{ij} + \mu_1 \mu_2$ .

3.3 其它性质

n 维正态分布的边缘分布是正态分布.
n 维正态分布的条件分布是正态分布.
n 维正态分布的边缘分布的和是正态分布.
$(\soneto{X}{n})$ 服从 n 维正态分布的充要条件是:
$\forall l_{i} \in R (i = 1, 2, \dots, n) : l_{1} X_{1} + l_{2} X_{2} + \dots + l_{n} X_{n} \sim N (μ, σ^{2}) .$
$\soneto{Y}{m}$ $X_i\, (i = \oneton)$ 线性函数 $(\soneto{Y}{m})$ 服从 m 维正态分布.
n 维正态分布各分量相互对立充要条件是它们两两不相关.

4 狄利克雷分布

4.1 基础概念

$\bm X \sim \mathrm{Dir}(\bm \alpha)$ .
Dirichlet 分布又称为多元 Beta 分布, 属于指数族分布.
多元 Beta 函数与 Gamma 函数的 Dirichlet 公式
$\begin{aligned} B (α) & = B (α_{1}, α_{2}, \dots, α_{n}) := \int \dots \int \prod_{i = 1}^{n} x_{i}^{a_{i} - 1} d x & (\sum_{i = 1}^{n} x_{i} = 1) \\ = \frac{Γ (α_{1}) Γ (α_{2}) \dots Γ (α_{n})}{Γ (α_{1} + α_{2} + \dots + α_{n})} = \frac{Γ (α_{1}) \dots Γ (α_{n})}{Γ (a_{0})} & (a_{0} = \sum_{i = 1}^{n} a_{n}) \end{aligned}$
$d\ (d \in \N^+)$ $d-1$ 正单纯形 $(1, 0, \cdots, 0), (0, 1, \cdots, 0), \cdots, (0, 0, \cdots, 1)$ 围成.
概率密度函数
$\begin{aligned} Dir (X ∣ α) & = \frac{1}{B (α)} \prod_{i = 1}^{d} X_{i}^{α_{i} - 1} = \frac{Γ (α_{0})}{\prod_{i = 1}^{d} Γ (α_{i})} \prod_{i = 1}^{d} X_{i}^{α_{i} - 1} (α_{0} = \sum_{i = 1}^{d} α_{i}, d \geq 3) \\ = \frac{Γ (α_{0})}{\prod_{i = 1}^{d} Γ (α_{i})} (\prod_{i = 1}^{d - 1} X_{i}^{α_{i} - 1}) (1 - X_{1} - \dots - X_{d - 1})^{α_{d} - 1} (‖ X ‖ = 1) \end{aligned}$
$\bm \alpha$ 分布参数 $d \ge 3$ 为随机变量的维度.
备注:
- 上式中的范数指 1-范数而非 ~~2-范数~~.
- $d$ 维支撑集 同 Dirichlet 公式中的积分域.
- $\mathrm{Dir}(\bm \alpha)$ $\mathrm{Dir}(\bm X \mid \bm \alpha)$ .
- $\bm X$ $n-1$ $\bm \alpha$ $n$ 维.
对称 Dirichlet 分布
- $\mathrm{Dir}(\bm X \mid \bm \alpha) = \dfrac{\Gamma(d \bm \alpha)}{\Gamma(\bm \alpha)^d} \dprod_{i=1}^d X_i^{\alpha_i - 1}$ .
- $\bm \alpha$ 在所有维度相同, 取值也被称为 浓度参数.
  - $d$ $d-1$ 维正单纯形上的均匀分布, 也被称为 平 Dirichlet 分布.
  - 当浓度参数大于 1 时, 对称 Dirichlet 分布是一个集中分布, 此时浓度参数越大, 概率密度越集中.
  - 当浓度参数小于 1 时, 对称 Dirichlet 分布是一个稀疏分布, 此时浓度参数越接近于 0, Giallo密度越稀疏.
累积分布函数
$F (b) = \int_{R_{d} \cap [0, b)} Dir (X ∣ α) d X, (b \in (0, 1])$

4.2 数字特征

众数
- $M(X_i) = \dfrac{\alpha_i - 1}{\alpha_i + \alpha_d - 2} (x_d + x_i)$ .
  $x_d + x_i = 1 - x_1 - \cdots - x_{i-1} - x_{i+1} - \cdots - x_{d-1}$ $x_i$ 无关.
- $M(X_i) = \dfrac{\alpha_i - 1}{\alpha_0 - d}$ .
  注: 这是所有分量都取到众数时的取值, 是上式的特例.
$E\pqty{\dprod_{i=1}^d X_i^{\beta_i}} = \dfrac{\Gamma(\alpha_0)}{\Gamma(\alpha_0 + \beta_0)} \dprod_{i=1}^d \dfrac{\Gamma(\alpha_i + \beta_i)}{\Gamma(\alpha_i)} = \dfrac{\Beta(\bm \alpha + \bm \beta)}{\Beta(\bm \alpha)}$ $\beta_0 = \dsum_{i=1}^d \beta_i$ .
- $E(X_i) = \dfrac{\alpha_i}{\alpha_0}$ .
- $\Var(X_i) = E(X_i^2) - E(X_i)^2 = \dfrac{\alpha_i(\alpha_0 - \alpha_i)}{\alpha_0^2 (\alpha_0 + 1)}$ .
- $\Cov(X_i, X_j) = E(X_iX_j) - E(X_i) E(X_j) = \dfrac{\alpha_i(\alpha_0 - \alpha_j)}{\alpha_0^2(\alpha_0 + 1)}$ .

4.3 其它性质

相关分布
- $p(X_i) = \mathrm{Be}(X_i \mid \alpha_i, \alpha_0 - \alpha_i)$ .
  备注:
  - 即 Beta 分布, 或 2 维 Dirichlet 分布.
  - 毫无关系 $F(x_i; \alpha_i, \alpha_0 - \alpha_i)$ .
- 联合分布
  $p (X_{i}, X_{j}) = Dir (X_{i}, X_{j} ∣ α), α = [α_{i}, α_{j}, α_{0}], i, j \in {1, 2, \dots, d} .$
  $X_i$ $X_j$ 的联合分布为 3 维 Dirichlet 分布.
作为概率分布的性质
- 共轭性: 多项分布的共轭先验是 Dirichlet 分布 (同等无知原则).
- 聚合性: 不懂.
- 中立性
  $(\soneto{X}{s}) \in \bm X$ $(X_{s+1}, \cdots, X_d) \in \bm X$ 相互独立：
  $\begin{matrix} (X_{1}, \dots, X_{s}) ⊥ X^{*}, X^{*} = (\frac{X_{s + 1}}{X_{s + 1} + \dots + X_{d}}, \dots, \frac{X_{d}}{X_{s + 1} + \dots + X_{d}}), \\ p (X^{*} ∣ X_{1}, X_{2}, \dots, X_{s}) = Dir (α^{*}), α^{*} = (α_{s + 1}, α_{s + 2}, \dots, α_{d}) . \end{matrix}$
- $d$ $\bm T = \Gamma(\bm T \mid \bm \alpha, 1)$ 归一化后的联合分布:
  $\begin{array}{ll} T_{i} = Γ (T_{i} ∣ α_{i}, 1), Z_{d} = \sum_{i = 1}^{d} T_{i} \\ X = \frac{1}{Z_{d}} (T_{1}, T_{2}, \dots, T_{d - 1}), \\ p (X) = Dir (α_{1}, α_{2}, \dots, α_{d}) . \end{array}$
信息测度

A.3 常用分布统计表

A.3.1 标准正态分布表

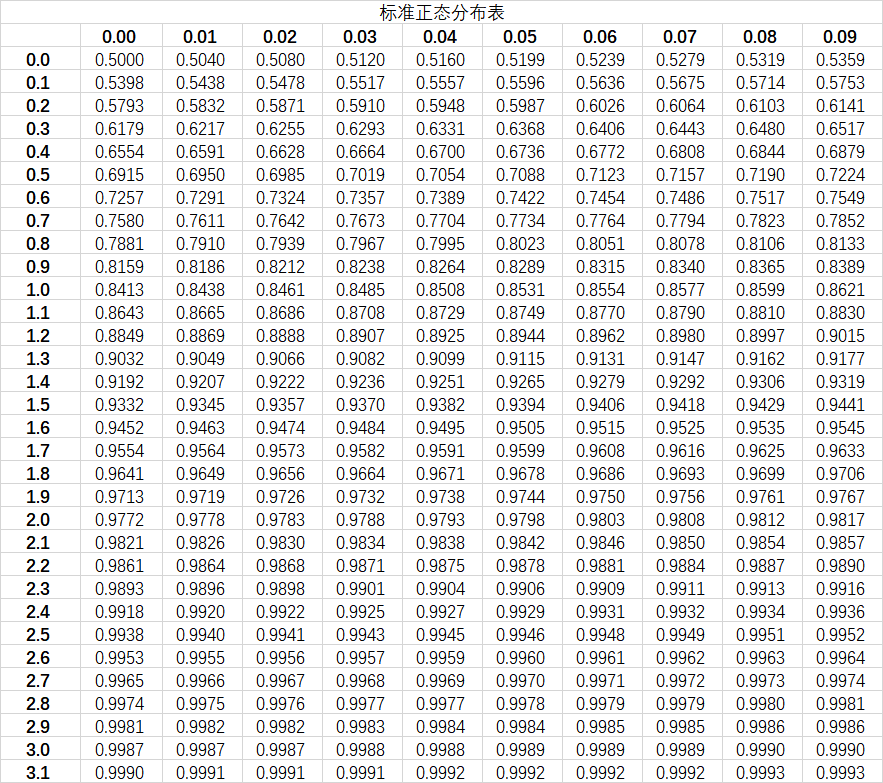
A.3.2 卡方分布表

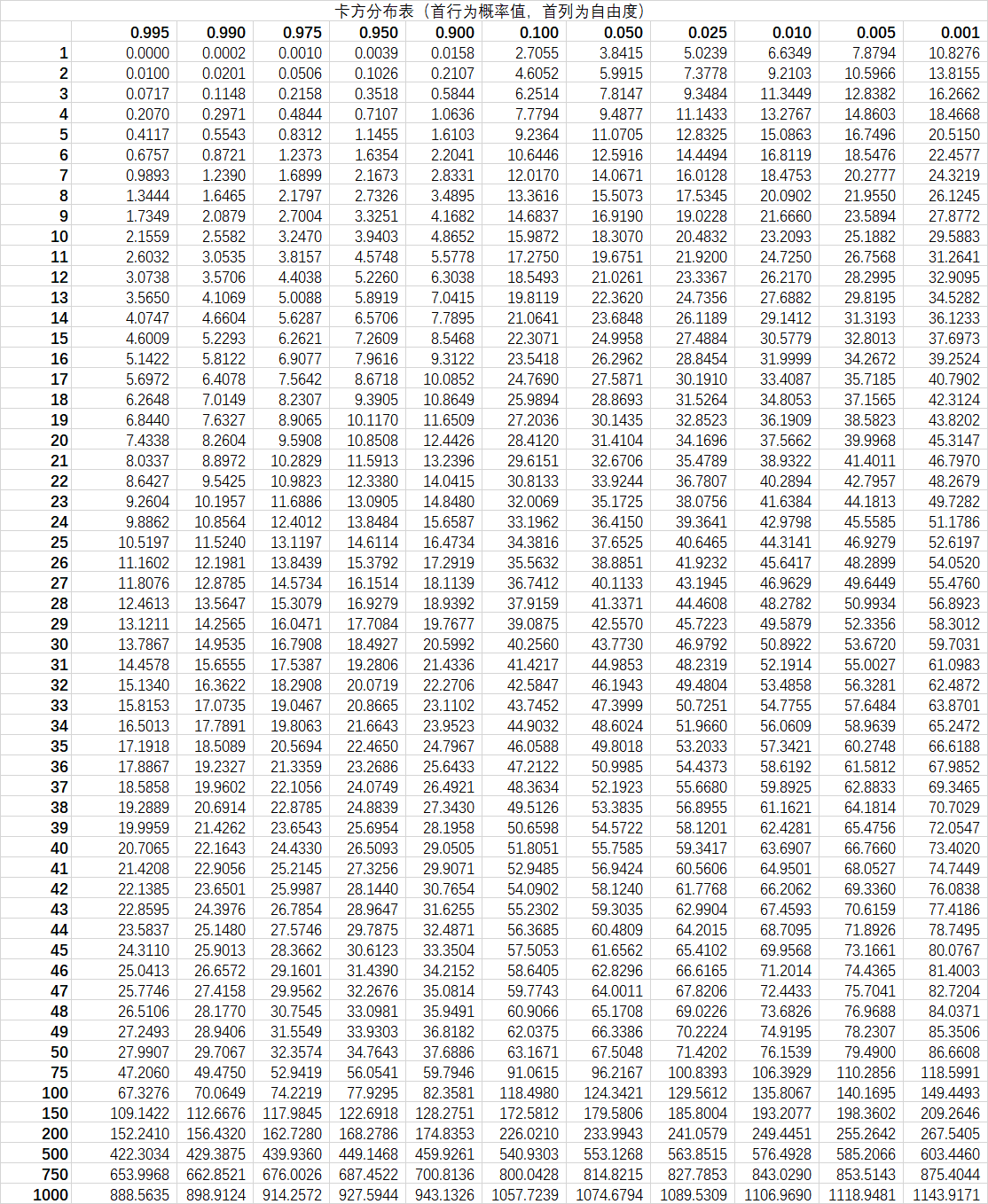
A.3.3 t 分布表

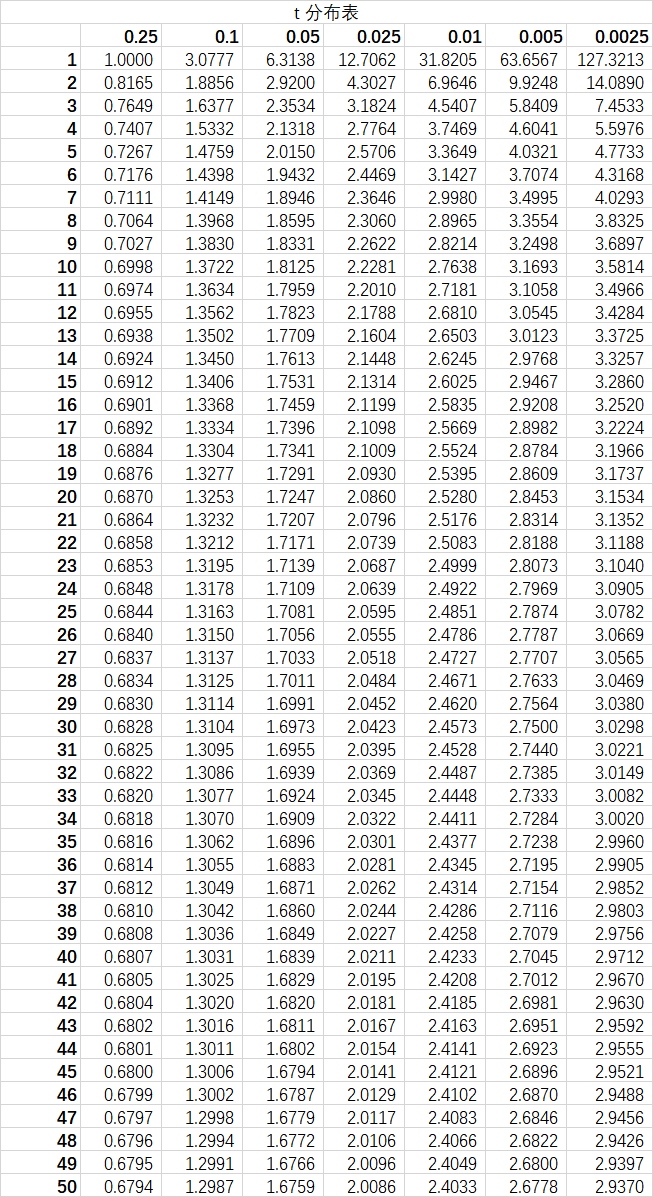
A.3.4 F 分布表

1 上 0.1 分位数

2 上 0.05 分位数

3 上 0.025 分位数

4 上 0.01 分位数

5 上 0.005 分位数

A.3.5 二项分布表

A.3.6 泊松分布表

A.4 数列和常数

A.4.1 数列

卡特兰数

Catalan 数又称明安图数.

递归定义

$C_0 = C_1 = 1$ .
$C_n = \dsum_{k=0}^{n-1} C_k C_{n-1-k}$ .

前几项值: 1, 1, 2, 5, 14, 43, 132, 429, 1439, 4862, 16796...

生成函数

$G(x) = \nosum C_n x^n$ $G^2(x) = \nosum C_{n+1} x^n$ , 故

\begin{aligned} {\begin{cases} G (x) = \sum_{n = 0}^{\infty} C_{n} x^{n} \\ C_{n} = \sum_{k = 0}^{n - 1} C_{k} C_{n - 1 - k} \end{cases} & \Rightarrow G^{2} (x) = \sum_{n = 0}^{\infty} C_{n + 1} x^{n} \\ {\begin{cases} x G^{2} (x) + 1 = G (x) \\ G (0) = 1 \end{cases} & \Rightarrow G (x) = \frac{1 - \sqrt{1 - 4 x}}{2 x} \end{aligned}

通项公式

$C_n = \dfrac{1}{n+1} \d \binom{2n}{n} = \dfrac{1}{2n+1} \binom{2n+1}{n}$ .
$C_n = \d\binom{2n}{n} - \binom{2n}{n-1}$ .
$C_n = \dfrac{1}{n+1} \dsum_{i=0}^n \binom{n}{i}^2$ .

证明

由生成函数泰勒展开即得.
由组合数定义即得.
$(1+x)^n\pqty{1 + \frac{1}{x}}^n = \dfrac{(1+x)^{2n}}{x^n}$ $\dsum_{i=0}^n \binom{n}{i}^2 = \binom{2n}{n}$ .

递推公式 $C_n = \dfrac{4n-2}{n+1} C_{n-1}$ .

证明由通项公式即得.

例题

$C_n = \dbinom{2n}{n} - \dbinom{2n}{n-1}$ 的场景.
1. $n \times n$ $(0, 0)$ $\dbinom{2n}{n} - \dbinom{2n}{n-1} = C_n$ 种.
2. $n$ $2n$ $C_n$ 种. (入栈出栈)
3. $2n$ $C_n$ 种.
$C_n = \dsum_{k=0}^{n-1} C_k C_{n-k-1}$ 的场景.
1. $n$ $n$ $C_n$ 种.
2. $n+2$ $n$ $C_n$ 种.

A.4.2 常数

卡特兰常数

级数定义与积分定义

\begin{aligned} G & = \sum_{n = 0}^{\infty} \frac{(- 1)^{n}}{(2 n + 1)^{2}} = \int_{0}^{1} \frac{\arctan x}{x} d x \\ = - \int_{0}^{1} \frac{\ln x}{1 + x^{2}} d x = \int_{0}^{+ \infty} \frac{\ln x}{1 + x^{2}} d x \\ = - \int_{0}^{\frac{π}{4}} \ln \tan x d x = \int_{0}^{\frac{π}{4}} \ln \cot x d x \\ = 0.915 965594177219015054603 515. . . \end{aligned}

常用积分

$\bqty{0, \dfrac{\pi}{2}}$ .
- 对数与三角
  - 正余弦 (区间再现后相加)
    - $\dint_0^{\tfrac{\pi}{2}} \ln\sin x \dx = -\dfrac{\pi}{2} \ln2$ .
    - $\dint_0^{\tfrac{\pi}{2}} \ln\cos x \dx = -\dfrac{\pi}{2} \ln2$ .
  - 正余切 (卡特兰常数定义)
    - $\dint_0^{\tfrac{\pi}{2}} \ln\tan x \dx = -G$ .
    - $\dint_0^{\tfrac{\pi}{2}} \ln\cot x\dx = G$ .
  - $1\pm{}$ 正余弦 (由半角公式即得)
    - $\dint_0^{\tfrac{\pi}{2}} \ln(1 + \sin x) \dx = \dint_0^{\tfrac{\pi}{2}} \ln(1 + \cos x) \dx = 2G - \dfrac{\pi}{2} \ln2$ .
    - $\dint_0^{\tfrac{\pi}{2}} \ln(1 - \sin x) \dx = \dint_0^{\tfrac{\pi}{2}} \ln(1 - \cos x) \dx = -2G - \dfrac{\pi}{2} \ln2$ .
  - $1+{}$ 正余切 (分区间利用结论)
    - $\dint_0^{\tfrac{\pi}{2}} \ln(1 + \tan x) \dx = G + \dfrac{\pi}{4} \ln2$ .
    - $\dint_0^{\tfrac{\pi}{2}} \ln(1 + \cot x) \dx = G + \dfrac{\pi}{4} \ln2$ .
- 幂与三角 (分布积分用结论)
  - $\dint_0^{\tfrac{\pi}{2}} \dfrac{x\sin x}{1 + \cos x} \dx = 2G - \dfrac{\pi}{2} \ln2$ .
  - $\dint_0^{\tfrac{\pi}{2}} \dfrac{x \sin x}{1 - \cos x} \dx = 2G + \dfrac{\pi}{2} \ln2$ .
  - $\dint_0^{\tfrac{\pi}{2}} \dfrac{x\cos x}{1 + \sin x} \dx = -2G + \pi \ln2$ .
  - $\dint_0^{\tfrac{\pi}{2}} \dfrac{x\cos x}{1 - \sin x} \dx = +\infty$ .
$\bqty{0, \dfrac{\pi}{4}}$ .
- 对数与三角
  - 正余弦 (相加减后解方程)
    - $\dint_0^\tfrac{\pi}{4} \ln\sin x\dx = -\dfrac{1}{2} G - \dfrac{\pi}{4} \ln2$ .
    - $\dint_0^{\tfrac{\pi}{4}} \ln\cos x\dx = \dfrac{1}{2} G - \dfrac{\pi}{4} ln2$ .
  - $1\pm{}$ 正余切 (区间再现后展开)
    - $\dint_0^{\tfrac{\pi}{4}} \ln(1 + \tan x) \dx = \dfrac{\pi}{8} \ln2$ .
    - $\dint_0^{\tfrac{\pi}{4}} \ln(1 - \tan x) \dx = \dfrac{\pi}{8} \ln2 - G$ .
    - $\dint_0^{\tfrac{\pi}{4}} \ln(\cot x + 1) \dx = G + \dfrac{\pi}{4} \ln2$ .
    - $\dint_0^{\tfrac{\pi}{4}} \ln(\cot x - 1) \dx = \dfrac{\pi}{8} \ln2$ .
  - 正余弦和差 (平方之后二倍角)
    - $\dint_0^{\tfrac{\pi}{4}} \ln(\cos x + \sin x) \dx = \dfrac{1}{2} G - \dfrac{\pi}{8} \ln2$ .
    - $\dint_0^{\tfrac{\pi}{4}} \ln(\cos x - \sin x) \dx = -\dfrac{1}{2} G - \dfrac{\pi}{8} \ln2$ .
- 幂与三角
  - $x\cdot{}$ 正余切 (分布积分用结论)
    - $\dint_0^{\tfrac{\pi}{4}} x\tan x \dx = \dfrac{1}{2} G - \dfrac{\pi}{8} \ln2$ .
    - $\dint_0^{\tfrac{\pi}{4}} x\cot x\dx = \dfrac{1}{2}G + \dfrac{\pi}{8} \ln2$ .
其它区间
- 幂与对数 (三角换元用结论)
  - $\dint_0^1 \dfrac{\ln(1 + x^2)}{1 + x^2} \dx = -G + \dfrac{\pi}{2} \ln2$ .
  - $\dint_0^1 \dfrac{\ln(1 - x^2)}{1 + x^2} \dx = -G + \dfrac{\pi}{4} \ln2$ .
  - $\dint_0^{\tfrac{\sqrt2}{2}} \dfrac{\ln x}{\sqrt{1-x^2}} \dx = -\dfrac{1}{2} G - \dfrac{\pi}{4} \ln2$ .