复变换-莫比乌斯变换与反演
第 3 章 莫比乌斯变换和反演3.2 反演3.2.1 复反演3.2.2 几何反演3.2.3 保持圆周3.2.4 作反演点3.2.5 保持角度3.2.6 保持对称性3.2.7 球面反演3.3 反演的应用3.3.1 相切圆问题3.3.2 正交对角线3.3.3 托勒密定理3.3.4 阿波罗尼奥斯定理3.3.5 笛卡尔定理3.3.6 阿波罗尼奥斯垫3.3.7 复笛卡尔定理3.3.8 Soddy-Gosset 定理3.3.9 鲍塞里耶铰链3.4 黎曼球面3.4.1 基本性质3.4.2 诱导映射3.4.3 球极射影公式3.5 莫比乌斯变换3.5.1 保持性质3.5.2 系数特点3.5.3 群性质3.5.4 不动点3.5.5 无穷远处的不动点3.5.6 交比3.5.7 变换性质3.6 莫比乌斯变换的矩阵3.6.1 矩阵与线性变换3.6.2 特征值与特征向量3.6.3 厄米特内积与正交3.6.4 酉矩阵与旋转3.7 可视化与分类3.7.1 变换的处理3.7.2 变换的分类3.7.3 乘子的解释3.7.4 抛物型变换3.7.5 乘子的计算3.7.6 乘子的解释3.8 分解3.9 单位圆盘的自同构第 4 章 微分学与伸扭第 5 章 微分学的几何研究5.1 CR 方程5.2 曲率5.3 天体力学
第 3 章 莫比乌斯变换和反演
3.2 反演
3.2.1 复反演
复反演
几何反演 (反演)
复共轭 (实轴反射)
分解与次序无关.
3.2.2 几何反演
几何反演
反演公式
由定义,
解之得,
基本性质
将平面分成两个分支.
分支边界的点为不动点.
对合性 (自逆性):
几何性质
相似
象距
3.2.3 保持圆周
记圆
保持圆周
若直线
它的反演是一个经过
象圆在
象圆半径
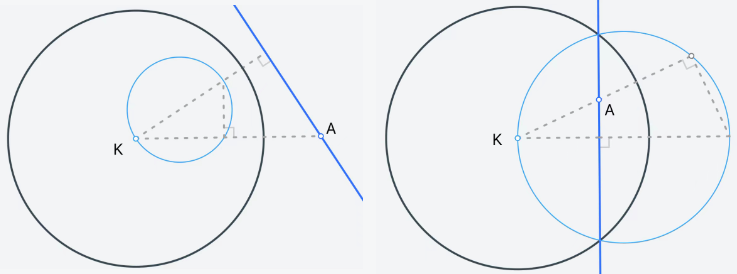
若圆
它的反演是一个不经过
象圆 -> 原圆
原圆 -> 象圆
1<img src='image\3.2.2 圆的反演.png' width=750>
映为自身
若直线
若圆
注: 一个圆的圆心与其反演圆的圆心不反演.
复反演将直角双曲线映为双纽线.
3.2.4 作反演点
法一 垂线与相似
证明
 垂线与相似.png)
备注 若点
法二 作圆与相似
证明
 作圆与相似.png)
备注 若点
法三 阿波罗尼斯圆
证明
 阿波罗尼斯圆.png)
备注 若点
法四 无刻度直尺
证明
 无刻度直尺.png)
备注 这也正是 (仿射变换后的) 20 年高考理科数学一卷的解析几何题 (的一般形式), 其中点
备注 若点
法五 利用正交圆
上述一正交圆可退化为过
反射可用相同的作法作出.
3.2.5 保持角度
共形映射: 保持每一点角度的大小和符号.
对于
偶数个反射 (反演) 的复合是共形映射.
反共形映射: 保持每一点角度的大小, 但符号相反.
反射和反演都是反共形映射.
奇数个反射 (反演) 的复合是反共形映射.
等角映射: 保持每一点角度的大小, 但符号未知.
3.2.6 保持对称性
对直线的反射能保持对直线的对称性.
对圆周的反射能保持对圆周的对称性.
因为反演映任一对正交圆周为另一对正交圆周.
3.2.7 球面反演
旋转 3.2.3 中的图像, 即得球面的结论:
球面反演具有对合性.
球面反演保持球面 (球面与平面).
球面反演保持圆周 (圆与线).
球面反演具有对称性 (反射反演与线性变换).
正交球面反演为正交球面.
3.3 反演的应用
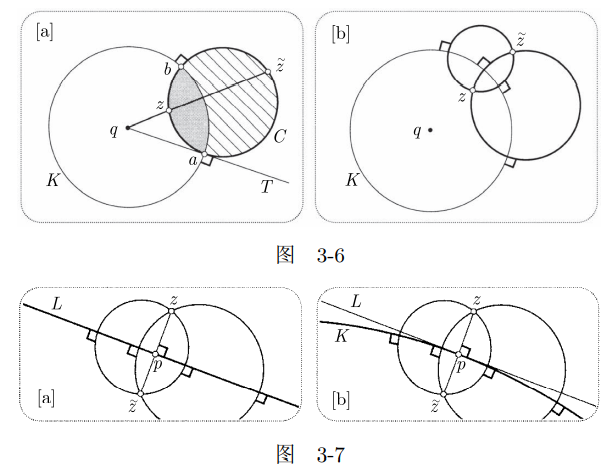
3.3.1 相切圆问题
如图, 由反演知:
设
3.3.2 正交对角线
如果一个四边形对角线正交于点
如图, 对角线正交, 故相邻蓝圆正交, 将被映为正交直线, 且平行于原四边形的对角线.
3.3.3 托勒密定理
证法一: 构造相似.
证法二: 复数运算.
证法三: 利用交比.
证法四: 利用反演.
这里使用反演进行证明:
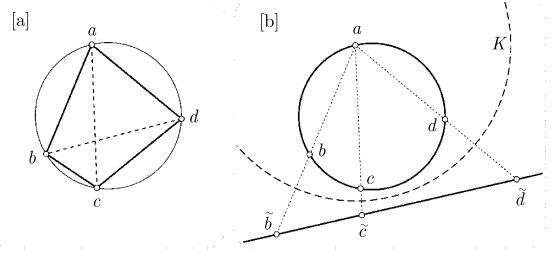
如图, 对以
备注 托勒密定理可以用来证明正余弦的加法公式. 实际上托勒密就是这么做的:
如左图,
于是可得正余弦的加减法公式.
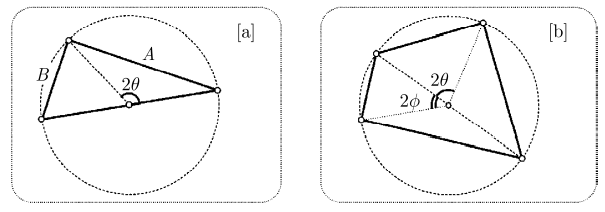
3.3.4 阿波罗尼奥斯定理
对于给定的三个两两相切 (但不公切于一点) 的圆
, 恰好存在两个圆与 均相切.
证明 对以
3.3.5 笛卡尔定理
假设四个两两相切的圆
的有向曲率分别为 , 则它们满足关系:
备注
曲率大小为曲率圆半径的倒数
如果两圆外切, 则二者曲率符号相同, 如果内切, 则相反.
证明 同阿波罗尼奥斯定理思路, 利用解析几何代入反演圆的半径公式即得.
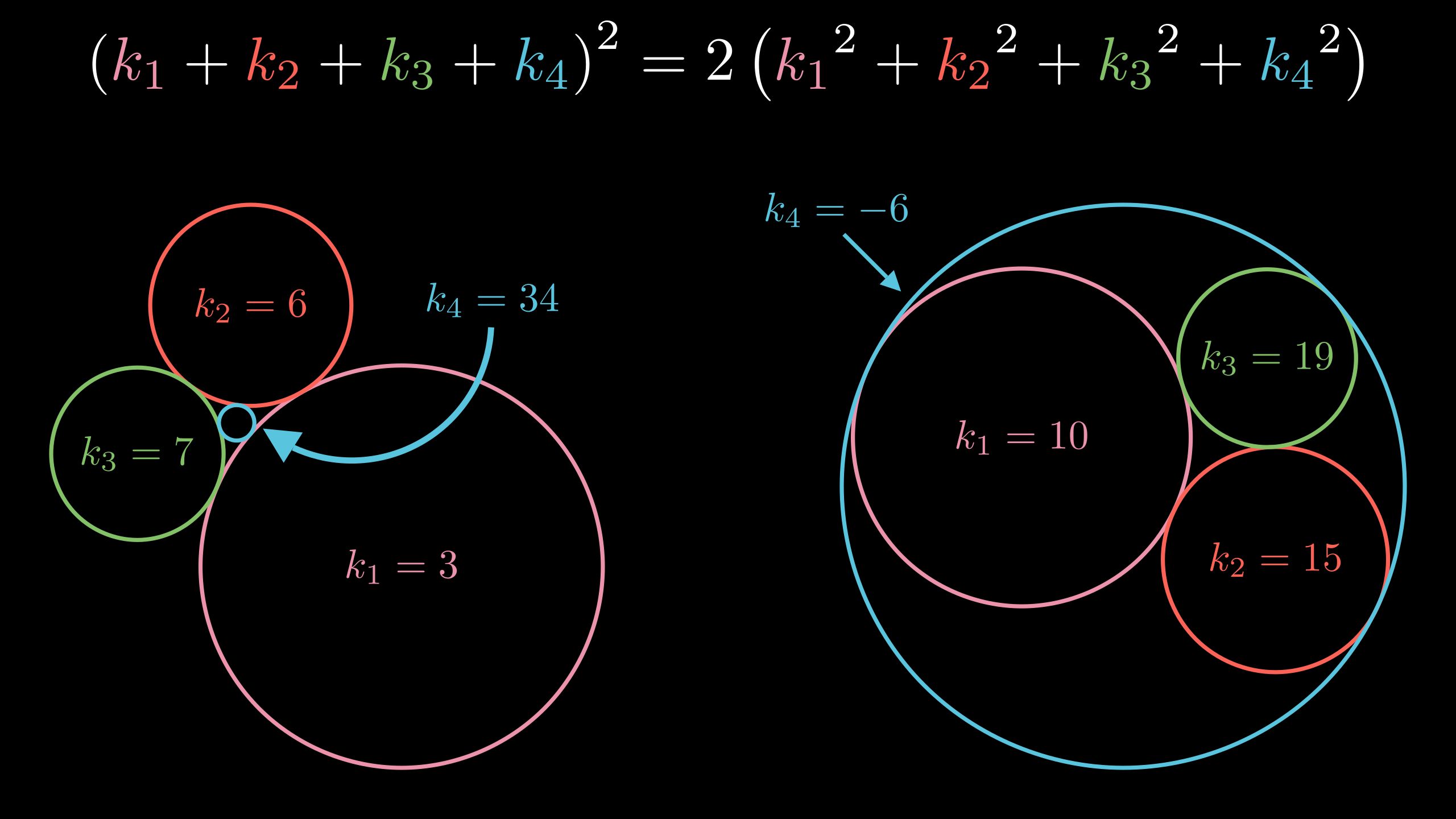
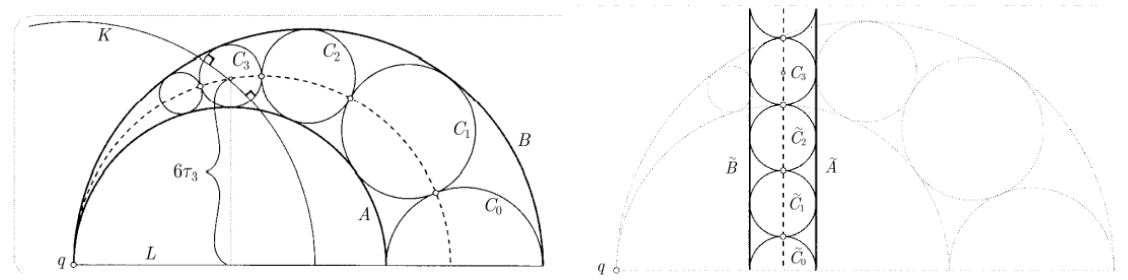
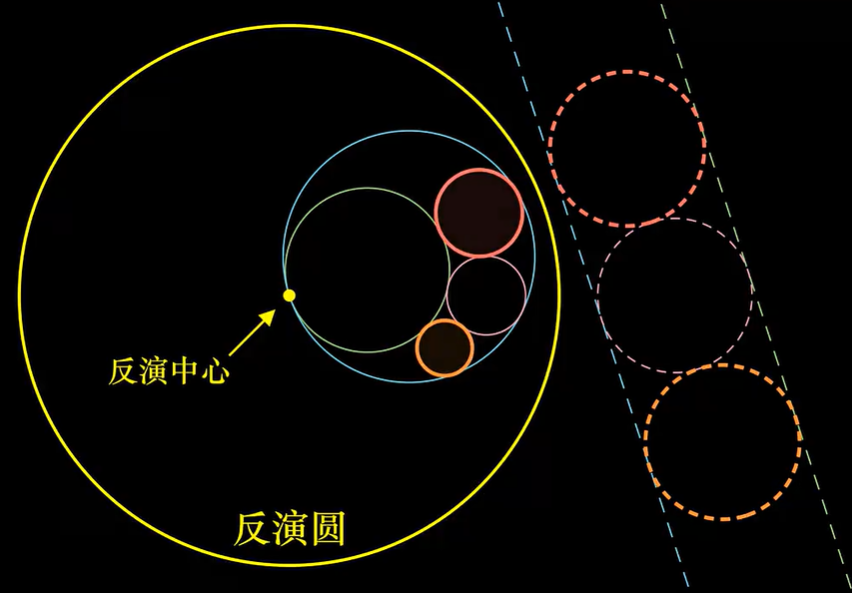
3.3.6 阿波罗尼奥斯垫
阿波罗尼奥斯垫
如给定圆
其中由笛卡尔定理得
阿波罗尼奥斯整垫
由笛卡尔定理与韦达定理得
若
若给定的
反之, 给定任意两个相切的圆, 可以作出其外公切圆, 使三圆直径共线, 从而得到相切圆问题.
黄金分割比
由上述四阶线性递推公式知, 当
令
其中前两根互为倒数, 后两根模为 1.
于是得相邻两项之比为
3.3.7 复笛卡尔定理
若复平面内四个两两相切的圆
的有向曲率分别为 , 圆心分别为 , 则它们满足关系
证明 与笛卡尔定理的思路相同, 解析剥蒜即可.
在莫比乌斯线性变换下, 上式仍然成立.
3.3.8 Soddy-Gosset 定理
若在
维欧氏空间中有 个两两相切且切点各异的 维球面, 则它们的有向曲率 满足关系:
证明 与二维的笛卡尔定理的思路相同, 解析剥蒜即可.
3.3.9 鲍塞里耶铰链
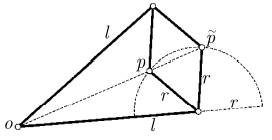
3.4 黎曼球面
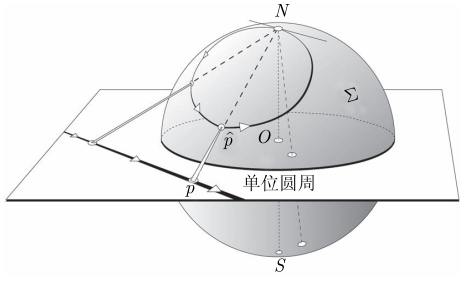
注意: 不同资料上的球极射影中心可能不同, 比如以图中的
注: 若先由
3.4.1 基本性质
复平面上直线的球极象
即黎曼球面
并且此圆周在
因此, 若从球内观察球面上角的方向, 那么球极射影是共形的.
黎曼球面与复平面是球面反演的, 因此球极射影保持圆周.
3.4.2 诱导映射
由
3.4.3 球极射影公式
记号约定
二维球坐标
若
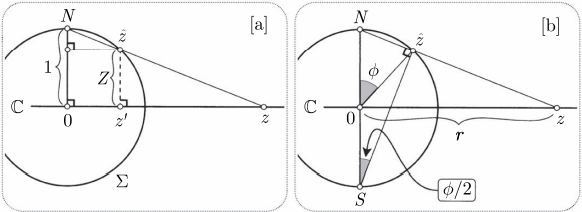
3.5 莫比乌斯变换
当
3.5.1 保持性质
换将圆周映为圆周.
莫比乌斯变换是共形变换.
对称原理: 若两点关于一圆周对称, 则映象亦如此.
定向圆周: 映有定向的圆周
3.5.2 系数特点
系数不唯一.
规范化: 即令
规范化的系数变为
存在唯一的莫比乌斯变换, 把任意 3 点变为任意 3 个其他点.
证明
3.5.3 群性质
逆变换
若
非奇异莫比乌斯变换的集合在复合运算下构成一个群.
3.5.4 不动点
即方程
上述方程的解为
规范化系数后为
非恒等映射的莫比乌斯变换最多有两个不动点.
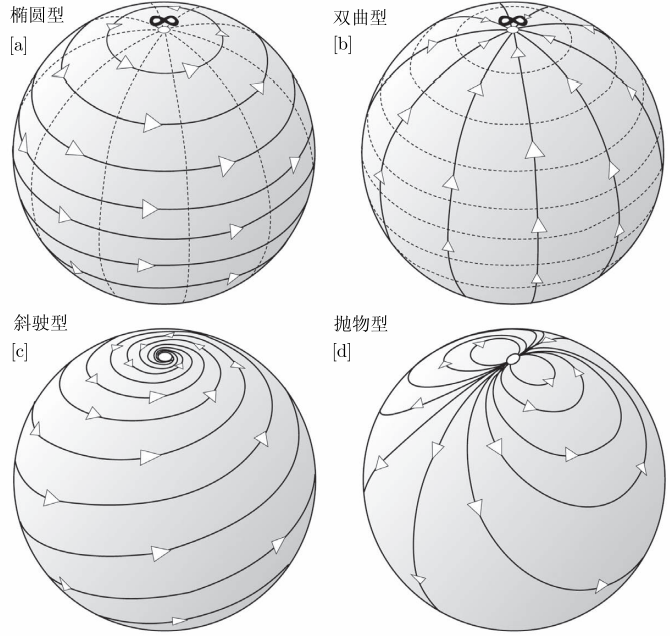
3.5.5 无穷远处的不动点
当
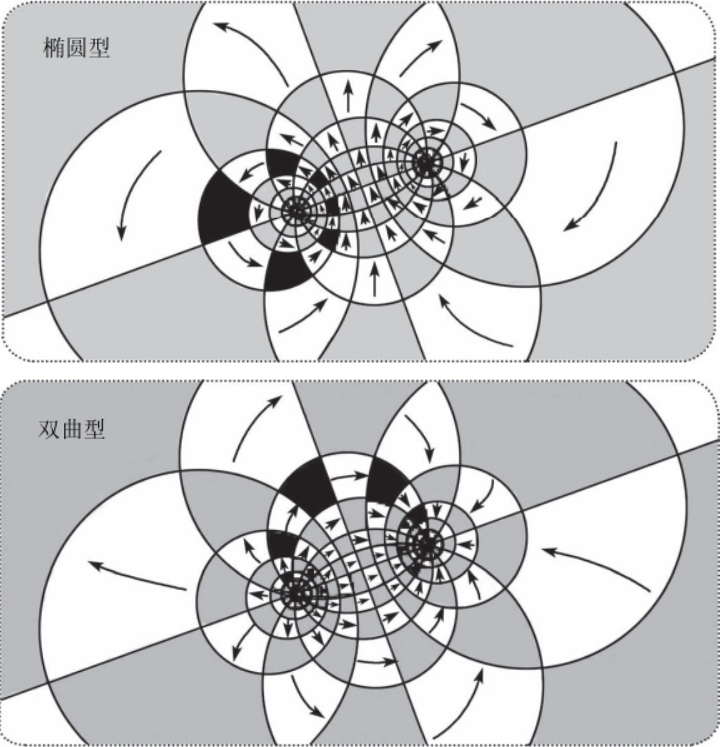
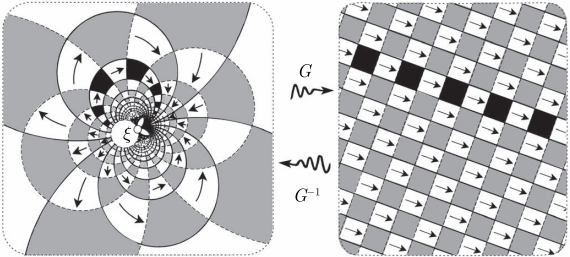
椭圆型 (旋转变换):
双曲型 (伸缩变换):
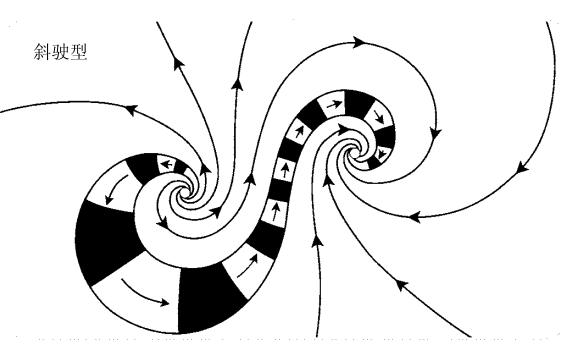
斜驶型 (相似变换):
抛物型 (平移变换):
3.5.6 交比
交比
将
有的资料上是分别映为
单比
变换
将
若莫比乌斯变换将
若交比相等, 则四点可用一个莫比乌斯变换映为另四点.
点的交比的排列组合
可以剥蒜, 如复分析笔记中一样.
也可以从变换的角度, 如可视化方法教材习题 16 中提供的思路.
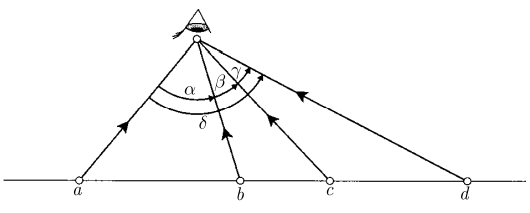
圆周
交比
圆周内域被映为实轴以上的半平面.
该圆周的方程为
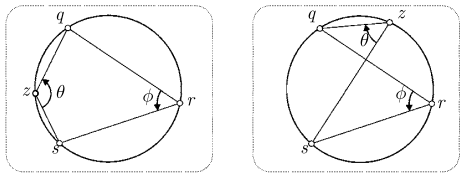
共线交比
共线四点
由此可见, 交比与四点所在共直线无关, 而由角度所唯一决定.
当上式值为 -1 时, 四点构成调和点列.
对称
若
证明:
3.5.7 变换性质
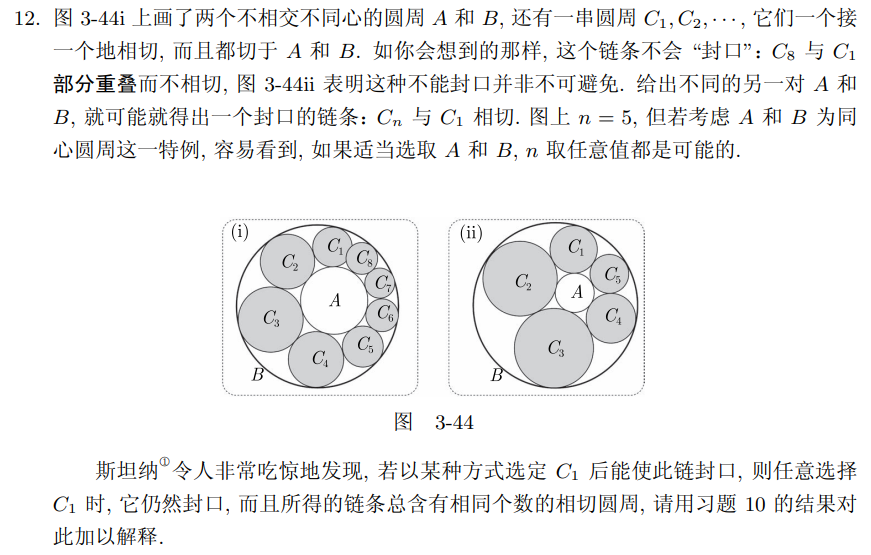
任意两个不相交且不同心的圆周可以用适当的默比乌斯变换映为同心圆周.
找到一对点
于是
上述性质的应用:
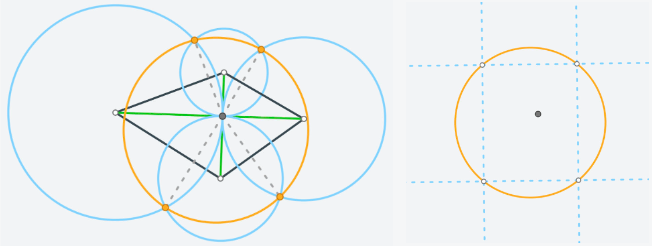
斯坦纳圆链
索蒂六球链

对于规范化的
同心圆周族当且仅当以
此时的象圆心为
方程为
3.6 莫比乌斯变换的矩阵
3.6.1 矩阵与线性变换
习惯上, 用圆括号表示
对于
莫比乌斯变换是
3.6.2 特征值与特征向量
特征方程
前者为行列式的值, 后者为迹.
3.6.3 厄米特内积与正交
内积
在
正交
当且仅当
记
3.6.4 酉矩阵与旋转
旋转: 使内积不变, 即
共轭转置
酉矩阵:
旋转矩阵等价于酉矩阵.
即
故黎曼球面的一般旋转可表示为
这些旋转及其对应的矩阵在复合运算下构成群.
3.7 可视化与分类
3.7.1 变换的处理
施泰纳圆网
设
则
在过不动点的直线上, 取点
则不动点关于
将施泰纳圆网通过
则一个不动点被映到
该莫比乌斯变换的不动点为
其中
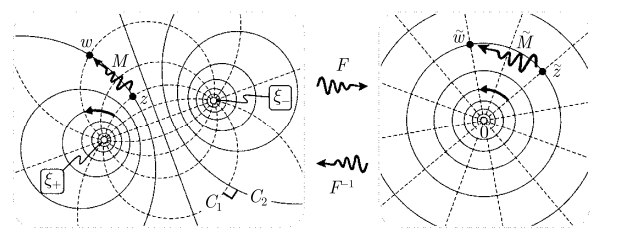
主要思想
3.7.2 变换的分类
椭圆型莫比乌斯变换
恒等映射是椭圆型.
只有椭圆型变换可能有有限周期.
双曲型莫比乌斯变换
排斥性不动点
吸收性不动点
斜驶型莫比乌斯变换
3.7.3 乘子的解释
记
称为莫比乌斯变换的 正规形式. 上式也可以写为
为减少歧义, 可以记
3.7.4 抛物型变换
只有一个不动点的莫比乌斯变换称为抛物型变换, 此时
如果
由于
其中不动点为
代入
3.7.5 乘子的计算
法一 (利用正规形式)
将
法二 (利用矩阵的迹)
由
由
或者对于未规范化的矩阵,
分类的判断
对于规范化的莫比乌斯变换
当
当
当
当
当
3.7.6 乘子的解释
若
3.8 分解
对广义圆周
偶数个反射的复合是一个莫比乌斯变换.
非斜驶型莫比乌斯变换可以表示为 2 个反射的复合.
斜驶型莫比乌斯变换可以表示为 4 个反射的复合.
莫比乌斯变换
椭圆型
其中
双曲型
其中
抛物型
其中
3.9 单位圆盘的自同构
自由度
一个复数变量最多有两个自由度.
最一般的莫比乌斯变换的集合的自由度为 6.
可等价地表示为
这些莫比乌斯变换的集合在复合运算下构成群.
先对一个正交于
由于
为使变换成为莫比乌斯变换, 需要偶数个反射. 而只有关于过
不动点
分类: 定义
当
当
当
黎曼映射定理:
定理: 任意单连通区域
即证
存在一个 3 参数的由
其它例子
将上半平面映为单位圆盘
最一般的莫比乌斯变换形如
其逆变换形如
上半平面的自同构
由于将实轴映为自身, 利用交比求解变换, 可得
由
第 4 章 微分学与伸扭
共形与解析
共形: 保持每一点角度的大小与符号.
解析: 每一点发出的无穷小复数都按同样的伸缩率和旋转度被伸扭.
孤立点共形
一个一定阶数的临界点被映到同阶的支点上.
一个保持方向的映射, 当且仅当它把无穷小圆周变为无穷小圆周时, 才是共形的.
复导数
柯西 - 黎曼方程组 (CR 方程)
利用对 x 与 y 的偏导相等.
利用解析函数在一点的效果相当于乘上一个复数的性质.
第 5 章 微分学的几何研究
5.1 CR 方程
Cart-Cart.
Cart-Polar.
Polar-Cart.
Polar-Polar.
5.2 曲率
曲率的解析变换
复曲率
注: 曲率
\kappa, 复曲率K的手写体.令
5.3 天体力学
有心力场
定义
力的中心
质点
性质
面积速度守恒
角动量守恒
两类椭圆轨道
当且仅当力场是线性的或服从平方反比律时, 才一定得到椭圆轨道.
线性吸引力场
引力中心位于椭圆中心.
建立复平面, 则微分方程为
其中
能量
平方反比引力场
引力中心位于椭圆焦点.
相互转换
每一个幂法则
一般说来, 正能量轨道不论是对吸引的还是排斥的力场